| Issue |
Int. J. Metrol. Qual. Eng.
Volume 13, 2022
|
|
|---|---|---|
| Article Number | 3 | |
| Number of page(s) | 15 | |
| DOI | https://doi.org/10.1051/ijmqe/2022002 | |
| Published online | 14 February 2022 | |
Research Article
On the performance of a Coriolis Mass Flowmeter (CMF): experimental measurement and FSI simulation
School of Science and Technology, University of Rwanda,
Kigali, Rwanda
* Corresponding author: bwgace@gmail.com
Received:
30
April
2021
Accepted:
3
January
2022
Computational methods that make use of single one-way Fluid Structure Interaction (FSI) for modeling the Coriolis Mass Flowmeters' (CMFs) operations are prone to inaccuracies. These errors are due to their limitations in describing a fully coupled fluid structure interaction. The aim of this study is to produce a CFD model of a CMF that uses an iterative two-way coupling of fluid structure interaction to accurately study its performance. The computational findings are benchmarked against accurate experimental measurements of the U-shape CFM. The deviation between the computed results and experimental measurements remains about 0.1% which is deemed acceptable. This reduction of uncertainties is largely attributed to the capability of the model to describe the effects of tube vibrations on the meter's operation.
Key words: Flow measurement / coriolis flowmeters performance / iterative two-way coupling / fluid structure interactions
© D.A. Gace, Published by EDP Sciences, 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Coriolis Flowmeters, CFMs, are flow measurement equipments which operate on the interaction between motions of the fluid being metered and vibrations of the pipe conveying fluid to produce the measurable effect. A CFM pipe undergoes undamped oscillations at one of its natural frequencies, mostly the first natural frequency, due to a harmonic excitation. For non-flow condition, both the inlet tube arm and the outlet arm oscillate in phase and two sensors symmetrically mounted on both sides of excitation point register the same displacements. However, if the fluid passes through the vibrating tube, a Coriolis force is generated as described by Gustave-Gaspard Coriolis in 1835 [1]. This force distorts the meter's vibrations pattern and induces a measurable effect as the difference between displacements of sensors' points or corresponding time shifts.
CFMs have been widely used in oil and gas industry for fuel bunkering and for Liquefied Natural Gas (LNG) metering owing to their high perceived accuracy and repeatability. Moreover, contrary to other measurement technologies whose primary measurement parameters are velocity, pressure or volume flowrates, CFMs directly measure the mass flowrates. Hence, in theory, their performance is supposedly independent of the fluids' thermal properties. However, viscosities of oil and potential air entrainments have been reported to have hindered normal meter operations [2–4].
Effective studies on CFM performance would require both numerical simulations and experimental measurements. Numerical simulation provides details on the fluid flow interacting with the vibrating tube. Numerical simulation on the CFM's operation allows approximating the masses of fluid flowing through and is useful for possible improvement on CFMs' design or layout. As such, numerical simulation can serve to increase the robustness of the CFM and its application range. On the other hand, experiments are realistic representative of actual scenarios on the coupled tube-fluid dynamics; thus, they provide calibration and validations for numerical computations.
As CFMs' principle involves interactions of fluid flow and vibrations of tube, their behaviors are likely to be affected by vibrational disturbances. Cheesewright et al. [5] listed the different types of vibrations that can contribute to errors on the meter measurements. These are: external vibrations, flow pulsations, disturbances due to interactions of driver mode with higher modes and rapid change of mass flowrates or densities (i.e. unsteady effect). Vetter and Notzon [6] found out that for CFMs operating under poly/monofrequency flow pulsations, the usual CFM characteristic equation does not hold. The erroneousness operation was identified to be a result of resonance of flow pulsations and tube oscillations at driver's frequency. In an experimental-assisted mathematical study, Svete et al. [7]asserted that pulsations at the same frequency as the driver frequency of a CFM only interfere with CFMs vibrations directly; while, pulsations at Coriolis frequency disturb meter dynamics through both direct and induced vibrational fluctuations. Similar to the second assertion of [7], Cheesewright and coworkers [8,9] affirmed that flow pulsations agitate the meter operations not only at one of natural frequencies, but also the frequencies equivalent to sum/difference of coriolis frequency and driver frequency as well as coriolis frequency minus the double of driver frequency corresponds to troubled oscillations. Separately, Cheesewright et al. [10] found that noise in meter's response due to flow pulsations can also lead to erratic outputs and hence error.
Like flow pulsations, external vibration of the same frequency as CFM's driver have been reported to interfere with the meter's operation [11]. Additionally, Cheesewright et al. [9] have shown that not only at the driver frequency, but at any frequency external vibrations can interfere with the meter's operation. Equally so, Clark and Cheesewright [12] identified external vibrations' (unconstructive) influences on the meter's readings at driver frequency, at Coriolis frequency and at a number of other discrete frequencies.
Therefore, to avoid these mentioned disturbances and more, characteristic modal shapes are assigned to currently available commercial CFMs in which they oscillate with least vulnerability to vibrational disturbances. These modal shapes consist of a set of specific modal frequency, comprising mostly the first natural frequency of a particular CFM, amplitude and direction of oscillation. For a numerical analysis on CFM operation, any inaccuracy in setting up the modal shape contributes to inaccuracies in predicting its performance, else the accuracy of simulation results mainly depend on the approach used to model the coupled dynamics of CFM tube and conveyed fluids.
A number of fluid structure interactions (FSI) based studies have been carried out to predict the performance of Colioris flow meters on measurement of mass flowrates or masses of fluid. Hemp [13] was probably the first to provide a detailed FSI model for a CFM by making use of beam theory (Harmonic beam model). The model has supposedly replicated CFM dynamics; however, its predictions considerably deviated from the experimental data and theoretical prospects for different fluids. Subsequently, Hemp and coworkers [14,15] extended the harmonic beam model into a weighting vector model. In addition to taking into account the influences of fluid flow on the system's dynamics, the normal velocity vector was modified to accommodate the effects of velocity profile. Still, the new model is restricted to predicting the velocity profile effects on CFM performance for measurement on inviscid fluids.
More recently Binulal et al. [16–18] directly coupled the fluid flow and tube oscillations into a single equation of motion to study the dynamics of CFM pipe conveying fluid. This method allows the determination of the influence of fluid flow on overall dynamics of the system including effects of added mass of the fluid, effect of pressure exerted on pipe's wall by the fluid and effect of centrifugal forces. But their studies did not take into account the possible influence of changes in structure oscillations to meter's operations and hence on accuracy of determined outputs. As such, deviation of up to 6.25% between computed results and references were observed.
A few other studies [3,19–22] have made use of iterative two-ways coupling of fluid structure interaction to identify the mechanism responsible for meter's atypical operation for low Reynolds number flow and mainly viscous flows. However, effects on FSI coupling method on the accuracy of predicted outputs have not been explored. As such, there is a need to analyze the effects of FSI coupling approach on the accuracy of computed results and to come up with an accurate numerical model of CMF that can complement experiments on determination of mass flowrates of fluids through CFMs. This provides the motivation of the present work to evaluate the contribution of FSI coupling method on the accuracy of numerical simulation on CMF performance with comparison to experimental measurements and calibration and to build an accurate model of CMF based on iterative two-way FSI coupling. Such model is of capital importance in metrological applications. In this study, a model analysis is conducted to determine a proper modal shape for oscillations of a CFM, a FSI based CFD Model of CFM is built and used to compute the mass flowrates of water through the CFM in the appropriate vibrational mode. Numerical results are validated with accurate experimental results of CFM200 at National Metrology Centre NMC flow laboratory and evaluated against requirements on accuracy on single-phase measurements as well as against the theories behind the meter's operation.
2 Methods
2.1 CFD modeling and simulations
The model considered for analysis consists of identical twin U-shape tubes. This study is centered on the CFM200. A CFD model of a single tube of CFM200 (Fig. 1) is considered for simulations and the results are extended to both tubes. The meter's pipes are made of 316L stainless steel of density 8070 g/cm3 and Young's modulus of elasticity 1.93 × 1011 Pa. Both dimensions and key properties of the meter tube are presented in Table 1. The CFM200 model was built in Autodesk Inventor Professional 2016 and imported to ANYSIS for simulations. In ANYSIS, the model is held XY plane of a fixed three dimensional XYZ frame of reference with the origin of the system of the coordinate coinciding with the point of application of the driver excitation. The tube's volume is 2.536810−0.005 m3 and its mass is 0.20472 kg. The outer diameter, the outer diameter and the pipe thickness are 30.6 mm, 28 mm and 1.3 mm respectively. Different meshes are generated on both the fluid and structure domains for mesh dependence test. Simulation is carried out for each of generated pair of meshes. This is first, to determine the mesh independent solutions for a number of inlet velocities and hence to find out the mesh for which the simulation results do not significantly change with change of mesh resolutions. Hence, Subsequent simulations used the proper mesh resolution for different inlet velocities.
Standard eigen value equation, equation (1) governs the model analysis for structures [23] (1)here M, C and K are mass matrix, damping matrix and stiffness matrix, respectively and F (t) is an external excitation force.
(1)here M, C and K are mass matrix, damping matrix and stiffness matrix, respectively and F (t) is an external excitation force.
Among n modes corresponding to n degrees of freedom of a system, the proper mode should matches up to maximum ratio of amplitudes of participating modes, equation (2)
 (2)
(2)
where F0 (ω1) is the amplitude of first natural modal shape while F0 (ωi) represents amplitudes of other modal shapes.
The governing equations for the fluid domain are the mass conservation equation, equation (3), and momentum equation, equation (4), in integral form, in three-dimensional spatial distribution. The governing equations were modified to include the effects of surrounding boundary motion [3,19,21,22,24,25].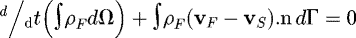 (3)
(3)
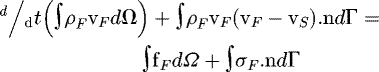 (4)where ρF, fF, σF ⋅ vF and vS are respectively; fluid densities, unity volume force acting inside the volume Ω, unity surface tension force, fluid velocity and surrounding boundary velocity respectively. And the boundary conditions are given as:
(4)where ρF, fF, σF ⋅ vF and vS are respectively; fluid densities, unity volume force acting inside the volume Ω, unity surface tension force, fluid velocity and surrounding boundary velocity respectively. And the boundary conditions are given as: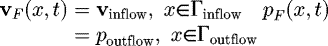
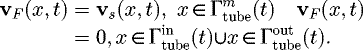
The structure‘s oscillations are modeled by Hamilton Variation principle equation (5). The Hamilton variation principle provides full information on the systems’ dynamics by use of action integral of a single function.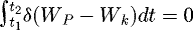 (5)
where WP andWk are total potential energy and total kinetic energy respectively. Their expressions are provided and described in [22,25,26]. The initial condition of structure's motion, assumed unstressed and unconstrained (ϵs (x, 0) = σs (x, 0)), consists of specific speed velocity, vs (x, 0) and acceleration as (x, 0) at t = 0. The boundary conditions are given as:
(5)
where WP andWk are total potential energy and total kinetic energy respectively. Their expressions are provided and described in [22,25,26]. The initial condition of structure's motion, assumed unstressed and unconstrained (ϵs (x, 0) = σs (x, 0)), consists of specific speed velocity, vs (x, 0) and acceleration as (x, 0) at t = 0. The boundary conditions are given as: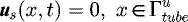

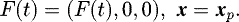
Uncoupled solutions on fluid and structure domains are to be coupled at the fluid structure interface, ΓFS, by setting up kinematic and dynamic constraints equation (6) [22] in order to simulate the overall dynamics of the fluid conveying tube.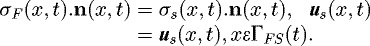 (6)
(6)
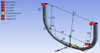 |
Fig. 1 CFD model of a U-shape tube: D1, D2, D3, D4, D5 are lengths of different sections of a CFM, D6 angle of bend of CFM pipe while A, B, C, D, E, F, G are key components on a CFM. The excitation, E is indicated by a yellow arrow in the z-direction. |
Dimensions (D1 to D6) and properties flow tubes: P1, P2, P3, P4, P5 and P6 are the density, Young modulus, thermal expansion, Poisson ratio, bulk and shear modulus, respectively.
2.1.1 CFD simulation procedure
The simulation uses components of ANSYS Workbench framework and count four stages: modal analysis, fluid flow analysis, structure transient analysis and fluid-structure coupling. Detailed procedures on simulation of fluid flowing through a CFM are presented in Figure 2. As can be seen, firstly, the modal analysis is carried out to determine a proper model shape in which the tube is forced to vibrate. Once a proper mode is determined, initial simulation is carried out separately on structure and on fluid domains and finally initial results are coupled and the operations are iterated until converged solutions are achieved.
The model analysis uses a program controlled solver of a mechanical Ansys Parametric Design Language (APDL) with default parameter values. In APDL, the CFM200 model is allowed to undergo translations along x, y, z axes and rotations about these axes.
In the fluid domain, the simulation uses general purpose computational fluid dynamic solver FLUENT16. A pressure-based viscous SST k-omega model was considered. A double precision convergence criterion for the continuity and momentum equations is set as 10−10. The fluid is water of density 998.2 kg/m3 and of kinematic viscosity 1003 × 10−6 kg/m s. For the boundary conditions, the pressure is set to zero at the outlet and inlet velocities are set for each nominal mass flowrates.
The structure oscillations are simulated in transient structure component of Ansys using APDL code. Simulations use a harmonic excitation force F (t) = F0sin(2πft)) applied at the middle point of the flexible tube to impose undamped oscillations of the tube. Where the amplitude of the harmonic excitation F0 is set at 25 μm and the frequency at which the tube oscillate, f, is the proper frequency described in Section (2.1.2.1).
In the system coupling component of ANYSIS workbench data transfers are created depending on FSI coupling method. While for one-way FSI coupling only one data transfer to transport the information from the fluid domain to the structure domain is created, for a two-way FSI the second is added to transport the information from the structure domain to the fluid domain. After an initial coupled solution, it is iterated up to 200 coupling steps corresponding to duration of 0.1 s. In each coupling step, number of coupling iterations is set to 5 to allow convergence in one coupling step while the time step is set to 0.5E–4s.
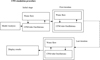 |
Fig. 2 Simulation chart: Model analysis and fluid flow coupled to tube oscillation iterative two-way fluid structure interactions. |
2.1.2 Post-processing of computational data
Numerical outputs are displacements of sensors locations presented as function of time. The main objective of this section is to determine the mass flowrates corresponding to difference of displacements registered at sensors' locations or to linked time shifts. Time shifts between oscillations at two sensors are determined from displacements, and converted into corresponding mass flowrates by mean of the characteristic equation of Coriolis flowmeter, equation
(7). The detailed derivation and description of the characteristic equation of Coriolis flowmeter was provided by Smith [27]. (7)where K is commonly known as meter factor; it represents the mass flowrate per unit time shift. The time shift Δt is calculated for a few points corresponding to displacements of the origin (see t = 0 in Fig. 9) and averaged. This can be achieved by use of linear interpolations on the points from either side of intersections of graphs with time axis. Thus the average time shift is given by equation (8).
(7)where K is commonly known as meter factor; it represents the mass flowrate per unit time shift. The time shift Δt is calculated for a few points corresponding to displacements of the origin (see t = 0 in Fig. 9) and averaged. This can be achieved by use of linear interpolations on the points from either side of intersections of graphs with time axis. Thus the average time shift is given by equation (8).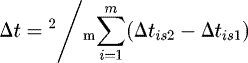 (8)where m is the number of interpolation points, and tis1 and tis2 are respectively determined by equations (9) and (10).
(8)where m is the number of interpolation points, and tis1 and tis2 are respectively determined by equations (9) and (10).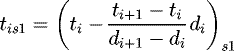 (9)
(9)
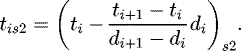 (10)
(10)
Subscripts s1 and s2 stand for sensor 1 and sensor 2 while i, i+1 rebel the first and the second of the two points considered for linear interpolation.
Different values of the meter are determined by using different models, equations (11) −(13). 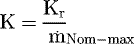 (11)
(11)
 (12)
(12)
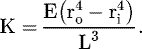 (13)
(13)
According to the Emerson Process Management [28], in the formula (11) , kr maximum frequency output for Micro Motion® Series 1000, 2000 and 3000 Series transmitters while 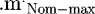 is the maximum nominal flowrate of the device. Equations (12) and (13) present analytical estimates of Coriolis meter factor, derived respectively by Smith [27] and Kazahaya [29]. Ks, L, rL, ro and ri are respectively spring constant, length of the meter (length of the meter leg), legs distance to central axis and tube radii.
is the maximum nominal flowrate of the device. Equations (12) and (13) present analytical estimates of Coriolis meter factor, derived respectively by Smith [27] and Kazahaya [29]. Ks, L, rL, ro and ri are respectively spring constant, length of the meter (length of the meter leg), legs distance to central axis and tube radii.
To evaluate any unit Under Test (UUT) against a corresponding reference the deviation,ϵ, between their outputs on a given proper B is calculated by equation (14) [30]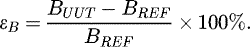 (14)
(14)
2.2 Experimental measurements
2.2.1 Experimental set-up
The experiments have been carried out on a large scale flow system with a U-shape Colioris flow meter at the National Metrology Centre (NMC) flow laboratory. An actual experimental set-up and its schematic representation that highlights the main elements of the system are presented in FIgures 3 and 4, respectively. The flow system consists of a fluid-storage tank, a pump, an air cylinder, flow condition indicators, U-shape Coriolis flowmeter, flow control valves, an in-line viscometer, a reference balance and flow pipes. Two tanks of volume V = 3 m × 3 m × 0.6 m, that can contain up to 4.32 m3 of fluid each, stock fluids that can be delivered to the flow system during the measurement processes.
Throughout the measurements, a 50RPM centrifugal pump pushes the fluid through the flow system from the tanks. A CFM measures the different fluid properties and flow parameters and presents outputs on a monitor for further post-processing. The pressure and differential pressure collected are at the upstream and downstream of the meter, separately. The flow is controlled by two types of control valves, multiple in-line valves that allow the imposition of a particular route to the fluid flow and a linear control valve that is used to regulate the nominal flowrates. Nominal flowrates were set within limits of CFM200 U-shape CFM i.e. from 50 l/min to 600 l/min. A 1PPM accurate reference balance is used to benchmark the CFM measurement results.
 |
Fig. 3 Actual experimental setup of the entire flow system with U-shape CFM, reference balance, fluid stocking tanks, fluid channeling pipes, sensor and flow regulating valves. |
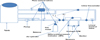 |
Fig. 4 Schematic experimental setup of the flow system indicating the main features like flow storage, flow measurements and flow regulators. T.I and P.I are the temperature indicator and pressure indicator, respectively. |
2.2.2 Experimental procedures
The main experimental steps are presented in Figure 5. First, the pump is switched on (after a pump control panel to allow fluid circulation in the system). A by-pass pipe prevents the pump for possible damages that may result from back flows. Reversing flow towards the tank may arise due to accidental-improper operations of the pump or pump failure. The fluid must flow through the CFM and the reference balance before it is allowed to flow back to the one of the two storage tanks. Only the valves in a particular flow path are to be opened while the valves in other flow routes remain fully closed. After a proper route is designed, it should be checked to ensure that there is no leakage in the entire flow system according to the designed flow route. After that, the compressor is turned on to supply the air to the pneumatic actuator, and a pneumatic actuator and a data communication system are turned on. Normally, empty start-up batch is likely to suffer from gas bubbles entrainment [31], thus the ventilating valves are to be opened to remove any traces of gases and the first batch of data is collected only after approximately 10 min of run time so that any remaining gas bubbles are removed from the pipe to the balance tank where they dissipate.
After both the CFM and reference balance data are collected, CFM readings are trimmed and balance tank is drained to get them ready for next measurement batch. For the subsequent measurements, the process keeps repeated and each time, after collection of five different sets of measurements at the same nominal flowrate, the nominal flowrate get adjusted until its maximum value, 600 kg/min, is reached.
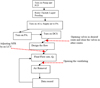 |
Fig. 5 Main experimental Procedures for measurements on a single phase fluid flow. PCP, ACo, CA, PA, DCS, LCV, GVF and NFR stand respectively for pump control panel, air compressor, air cylinder, pneumatic actuator, data communication system, gas volume fraction and nominal flowrate. |
3 Results
The dependence of the computational results on grid resolutions is tested as shown in Figure 6. The test evaluates the variation on computed mass flowrates for seven different grids for both structure and fluid domains and for three different inlet velocities. The number of elements generated on the fluid domain were 1904, 5610, 8241, 15611, 17487, 18023, 36960 and were consecutively paired to 360, 850, 1364, 5323, 10200, 14400, 20511 elements generated on the structure domain. As usual, the low and large numbers of cells corresponding to coarse and fine grid resolutions respectively. Pairs of grid resolutions are labeled by 1–7 and simulations were carried out for each mesh duo. Inlet velocities were set to 0.676 m/s, 3.382 m/s and 8.117 m/s. As shown, there was no significant change observed on computed mass flowrates for mesh duo 4–7. Thus, the 4th mesh pair was considered for further computations in this study.
Table 2 recapitulates the outcomes of a modal analysis. In the table, vibrational frequencies and ratios of amplitudes of participating modes are presented for six different degrees of freedom of the CFM tube. These degrees of freedom correspond to three translational motions in x, y and z directions and three rotational motions about x, y and z axes. It can be seen that a first modal frequency of 93.467 Hz corresponds to a ratio of amplitude of 1 only for a translation in the z-directions, elsewhere maxima ratios of candidate amplitudes match up with higher modal frequencies and in directions other than translation along the z-axis. One may note from the table of a significant ratio of amplitude, 0.471, associated with the fifty mode frequency in z-direction.
In Figure 7, the CFM is represented in the optimal vibrational mode. It is proven beforehand (see Tab. 2) that the proper model shape for CFM tube corresponds to undamping-harmonic oscillations in z-direction at the frequency of 93.467 Hz as presented in this figure. Figures 8 and 9 plot the displacements at sensors' locations as function of time for the tube oscillating under a continuous excitation in that mode. Figure. 8 presents the displacements registered by both sensors for non-flow condition, while Figure 9 shows the displacements at the same points when water flows through the meter tube at 7.305 m/s. While there is no difference noted between the outputs of the two sensors in Figure 8, in Figure 9 displacements differ. The difference between displacements at both sensor locations is equivalent to a time shift of 4.86E–05 seconds and to mass flowrate of 539.73 kg/min.
Figure 10 relates mass flowrates to time shifts between on sensors' oscillations. From the figure, numerically determined mass flowrates are shown to linearly correlate to the time shifts with a constant slope. The slope value in the graph corresponds to the CFM meter factor, K in the CMF characteristic equation (7) in Section 2.1.2. The results in Figure 10, moreover, show that the CFM200 model is able to track the analytical solution of the characteristic equation of coriolis flow meters. Although, it worth to be noted that the meter factor is function of CMF's material properties, meter's dimensions and transmitter technology. Thus, the method by which it is determined affects the numerical results. Figure 11 compares the mass flowrates calculated for different values of the meter factor, K to experimental measurements. The values of the meter factor are obtained from equations (11)–(13). Mass flowrates calculated based on meter factor's values obtained from numerical models Smith (1980) and Kazahaya (2014), represented by equations (12) and (13), noticeably deviate from experimental results. Contrarily, the mass flowrates calculated on basis of (Emerson, 2014) model presented (see Eq. (11)) are the most accurate as compared to experimental results.
Experimentally measurements used to validate computational results in Figure 11 need to be certainly accurate. Thus, mass measured by a CMF are benchmarked to mass flowrates measured by a 1 PPM reference balance in Table 3 to verify their accuracy. The table illustrates that masses measured by both the reference and the meter under the test agree with each other at more than 99.9% i.e. with a maximum deviation of 0.10% only. This confirms the potential of CMF outputs to be used as baseline for evaluation of the CMF200 model performance.
Along the lines of accuracy of the CMF model performance, Figure 12 evaluates the numerical results against accuracy requirements. The figure compares deviation between numerically predicted and experimentally measured mass flowrates to the required accuracy for F series CFM on measurement on single phase flow. According to the figure, for each of the sample points, the deviation remains within ± 0.1% of total mass flowrates.
 |
Fig. 6 Mass computed flowrates for different grid resolutions and inlet velocities: (a) vin = 0.676 m/s, (b) vin = 3.382 m/s and vin = 8.117 m/s. |
Modal analysis: thirty-six possible modes corresponding to six degrees of freedom and six modal frequencies with corresponding amplitude ratios, r.
 |
Fig. 7 Proper mode of U-shape CFM corresponds to its oscillations at first natural frequency 93.467 Hz in z-directions. |
 |
Fig. 8 Displacements of the tube oscillating under excitation force only. No flow flowing through the pipe. Displacement at sensor 1 and sensor 2 are plotted against time. |
 |
Fig. 9 Displacements at sensor locations for the tube oscillating under excitation force and fluid flow through the pipe at a velocity of 7.305 m/s. |
 |
Fig. 10 Variation of mass flowrates with time shifts between sensors. |
 |
Fig. 11 Model validation: Mass computed mass flowrates plotted against measured mass flowrates for different values of the meter factor K. |
Mass measured by a CFM benchmarked to mass measured by a reference balance and corresponding measurement error for a CFM.
 |
Fig. 12 Deviation between simulation results and measurements (green dots) evaluated against acceptable error limits. |
4 Discussions
According to the manufacturer, the proper modal frequency of U-shape CFM200 is 93.476 Hz, while in this, the optimal model frequency of the CFM200 model was found to be fd = 93.467 Hz. The estimated frequency differs from the actual one by 0.0096% only. That means that the built CFD model is able to precisely replicate the meter oscillation patterns of the actual meter. Moreover, Table 2 shows that out of the 36 possible natural modes of the CFM, the first natural frequency corresponds to the ratio of participation factors of 1 for translation in z-direction. Therefore, driving the meter at its first natural frequency in along z-direction allows for optimal use of exciter's energy and eliminates potential disturbances of modes with different directions to translation in z-direction. Even though the translation along z-axis is associated with significant amplitude ratio for the fifth higher modal frequency, its probability to interfere the meter's oscillations is limited. This is due to the fact that the mentioned modal frequency is not a multiple of the first natural frequency.
In addition to the capabilities of the model to replicating actual meter vibrations, the results demonstrate that the model depicts the theory underlying typical CFM's operations. Figure 8 and Figure 9 prove that, as expected, for empty CFM vibrating at its first natural frequency, there is no difference observed between displacements of sensor at the inlet leg and sensor outlet leg (see Fig. 8). However, when water flows through the oscillating tube sensors at the inlet and sensor at outlet register different displacements. The difference of displacements at sensor locations thanks to the interactions between the Coriolis forces and inertia force, see also [20]. The flow of fluid induces Coriolis forces of opposite directions at the inlet sensor and outlet sensors [32]. Unlike these apparent Coriolis forces, the tube inertia's forces have the same directions at the inlet and the outlet. Thus the Coriolis forces enhance the effects of inertia forces at one sensor location while opposing them at another sensor's location. These interactions distort symmetry of oscillations leading to difference between readings of the sensor at the inlet and the sensor at the outlet as can be seen on Figure 9.
In addition to depending on the time shifts as shown in Figure 10, CMF outputs also vary with the its material and its size. The effects of both meter's material properties and dimensions are comprised in the meter's factor, K. Hence, the method of by which the value of meter factor is determined (11))–(13) also affects the accuracy of computed mass flowrates. Figure 11 compares computed mass flowrates for different values of the meter factor. The figure shows that Emerson model [Eq. (11)] allows obtaining matches of experimental results.
However, mitigating the error associated determination of the meter factor does not completely assure accurate numerical results; the method of coupling the interaction between fluid flow and tube dynamics at fluid-structure interface bears main influences on accuracy of computed mass flowrates. Table 4 evaluates accuracy of computational results for both one-way and two-ways FSI coupling based simulations of FSI with respect to experimental measurements. As can be seen, for one-way FSI coupling the maximum deviation between numerical and experimental results is about 8%; but for the simulation based on two-way coupling of fluid structure interaction the maximum deviation is 0.1%. The iterative two-ways coupling based simulation allows achieving most accurate simulation results due to the fact that it properly represents the meter operations. In addition to counting on influence of fluid flow on structure oscillations, as the one-way coupling model does, two-ways coupling of fluid structure interactions counts on influences of every changes on tube oscillations on the numerical outputs.
In this study, owing to use of two-ways coupling of fluid structure interaction, simulation results meet theoretical expectations and accuracy requirements. In fact, as can be seen on Figure 10 that relate flow induced time-shifts and computed mass flowrates, computed results match the CFM's characteristic relation (Eq. (7)). Similarly, the meter's sensitivity (K*) remains constant (see Fig. 13) as required for a proper-linear operation CMF [33]. The sensitivity K* of a flow meter mathematically equals to the inverse of the meter factor, K. When the sensitivity remains constant, it is an indication of a steady operation for a CMF. Particularly in this study, a two-way FSI coupling a two-way coupling of FSI allowed to maintain a constant sensitivity for the CFD model of the CMF and hence to maintain a stable performance of the meter.
This provides the meter's model with smooth-constant operation. Contrarily, when a one-way coupling is used to represent the interactions between the oscillating tube and the fluid flowing through the tube, the sensitivity of CMF model fluctuates and noticeably drops. Such variations in sensitivity of the model explain observed inaccuracies in computed mass when the method was used.
In addition to agreeing with theories on CFM operation, the two-way FSI based CFD model concurs with experimental measurements. Figure 11 indicates that numerical results compare well with experimental measurements unless affected by the method of determination of the meter factor. It is worthwhile to note that in order to authenticate CMF experimental measurements, served as a secondary reference in this analysis, mass measured by a CMF were benchmarked to mass measured by means of a reference (Tab. 3). From the table, it can be seen that on maximum CFM measurements by deviated less than 0.1% from references. Given such small deviations one can conclude that CFMs measurement results are suitable to serve baseline while evaluating simulation results. Deviations between computed and measured mass flowrates (Fig. 12) fall within the range that is acceptable according to requirements on accuracy of F series CMFs. According to that accuracy requirement, the maximum magnitude of error on single phase flow should not exceed 0.1 percent of the total mass flowrates. The figure shows that simulating CFM operation by making use of an iterative two way coupling of FSI at the fluid and structure domains interface allows fulfilling that accuracy requirement on measurement single-phase flows.
Both numerical simulation and experimental analysis express accurate performance of CMFs on measurement on single phase flow. It is to be noted, however, that numerical simulation requires a two way FSI coupling of interactions to allow both transfer of information from fluid domain to the structure domain and vice versa in order to produce accurate results. In this study, it is seen that a two way FSI coupling based CMF model accurately and consistently replicate the operation of a commercial meter; thus it may be used as an alternative or supplemental baseline to costly experiments for further studies in the field of flow measurements as well as for industrial applications such as fuel bunkering and oil and gas metering among others.
Mass flowrates and meter errors for both one-way and two-way FSI simulations.
 |
Fig. 13 Sensitivity of the CMF model computed with both a two way and a one-way FSIs. |
5 Summary
In the oil and gas industry, fuel bunkering and LNG metering requires irrefutable and accurate measurement of fluid mass flowrates to avoid commercial losses. As measuring devices, CFMs outperform other measurement technologies due to their ability to directly measure mass flowrates. Given the high cost of these equipments, numerical simulations are needed to supplement laboratory experiments and field measurements in both research and industrial applications. The currently available numerical methods pay less attention to effects change in CMF oscillations on overall coupled fluid-tube dynamics. This leads to significant inaccuracies in numerical outputs. This study analyses the performance of CMFs using of CFD modeling based on iterative two-ways FSI and experimental measurements. It is found that:
Both experimental measurements and numerical simulations using two-ways FSI coupling prove that CFMs meet accuracy requirements on measurement on single-phase water flow (Tab. 3, Fig. 12, Tab. 4).
Simulations using a two-way FSI coupling provide the CMF model with capability to comply with theory behind CMFs operation (Tab. 2, Figs. 8–10), with ability to agree experiments (Figs 11 and 12, Tab. 4), with optimal accuracy (Tab. 4, Fig. 12) and with steady performance (Fig. 13).
A two-way iterative coupling of FSI reciprocally accounts on influences of fluid flow on structure dynamics and influences of tube oscillations on fluid flow; hence, it is required to enhances the accuracy of numerical predictions.
References
- G.G. Coriolis, Mémoire sur les équations du mouvement relatif des systèmes de corps: Bachelier (1835) [Google Scholar]
- M. Henry, M. Tombs, M. Duta, F. Zhou, R. Mercado, F. Kenyery, J. Shen, M. Morles, C. Garcia, R. Langansan, Two-phase flow metering of heavy oil using a coriolis mass flow meter: a case study, Flow Measur. Instr. 17, 399–413 (2006) [CrossRef] [Google Scholar]
- R. Luo, J. Wu, S. Wan, Fluid-structure coupling analysis and simulation of viscosity effect on Coriolis mass flowmeter, in APCOM & ISCM, 11-14th December, Singapore, 2013 [Google Scholar]
- A.F. Skea, A.R.W. Hall, Effects of gas leaks in oil flow on single-phase flowmeters, Flow Measur. Instr. 10, 145–150 (1999) [CrossRef] [Google Scholar]
- R. Cheesewright, C. Clark, D. Bisset, The identification of external factors which influence the calibration of Coriolis massflow meters, Flow Measur. Instrum. 11, 1–10 (2000) [CrossRef] [Google Scholar]
- G. Vetter, S. Notzon, Effect of pulsating flow on Coriolis mass flowmeters, Flow Measur. Instr. 5, 263–73 (1994) [CrossRef] [Google Scholar]
- A. Svete, J. Kutin, G. Bobovnik, I. Bajsić, Theoretical and experimental investigations of flow pulsation effects in Coriolis mass flowmeters, J. Sound Vibr. 352, 30–45 (2015) [CrossRef] [Google Scholar]
- A. Belhadj, R. Cheesewright, C. Clark, The simulation of coriolis meter response to pulsating flow using a general purpose F.E. code, J. Fluids Struct. 14, 613–34 (2000) [CrossRef] [Google Scholar]
- R. Cheesewright, A. Belhadj, C. Clark, Effect of mechanical vibrations on coriolis mass flow meters, J. Dyn. Syst. Measur. Control Trans. ASME 125, 103–113 (2003) [CrossRef] [Google Scholar]
- R. Cheesewright, C. Clark, Y.Y. Hou, The response of Coriolis flowmeters to pulsating flows, Flow Measur. Instru. 15, 59–67 (2004) [CrossRef] [Google Scholar]
- C. Clark, R. Cheesewright, Experimental determination of the dynamic response of Coriolis mass flow meters, Flow Measur. Instru. 17, 39–47 (2006) [CrossRef] [Google Scholar]
- C. Clark, R. Cheesewright, The influence upon Coriolis mass flow meters of external vibrations at selected frequencies, Flow Measur. Instru. 15, 33–42 (2003) [CrossRef] [Google Scholar]
- G.S.J. Hemp, Modelling of the Coriolis Mass flowmeter, J. Sound Vibr. 132, 473–89 (1989) [CrossRef] [Google Scholar]
- J. Hemp, L.A. Hendry, The weight vector theory of Coriolis mass flowmeters — Part 2. Boundary source of secondary vibration, Flow Measur. Instru. 6, 259–64 (1995) [CrossRef] [Google Scholar]
- J. Hemp, The weight vector theory of Coriolis mass flowmeters, Flow Measur. Instru. 5, 247–253 (1994) [CrossRef] [Google Scholar]
- B.R. Binulal, A. Rajan, S.R. Abhilash, J. Kochupillai, K. Heuy Dong, Mass flow prediction of the Coriolis meter using C0 continuous beam elements, J. Therm. Sci. 24, 398–402 (2015) [CrossRef] [Google Scholar]
- B.R. Binulal, A. Rajan, J. Kochupillai, Dynamic analysis of Coriolis flow meter using Timoshenko beam element, Flow Measur. Instru. 47, 100–109 (2016) [CrossRef] [Google Scholar]
- B.R. Binulal, A. Rajan, M. Unnikrishnan, J. Kochupillai, Experimental determination of time lag due to phase shift on a flexible pipe conveying fluid, Measurement 83, 85–95 (2016) [Google Scholar]
- V. Kumar, M. Anklin, Numerical simulations of coriolis flow meters for low reynolds number flows, MAPAN 26, 225–35 (2011) [CrossRef] [Google Scholar]
- V. Kumar, M. Anklin, B. Schwenter, Fluid–structure interaction (FSI) simulations on the sensitivity of Coriolis flow meter under low Reynolds number flows, in 15th International Flow Measurement Conference 2010, number flows in straight tube coriolis flowmeters. XX IMEKO World Congress:Metrology for Green Growth. Busan, Republic of Korea 2012. p. 1674–7. [Google Scholar]
- R. Luo, J. Wu, S. Wan, Numerical study on the effect of low Reynolds FLOMEKO 2010, October 13, 2010 − October 15, 2010. Taipei, Taiwan: IMEKO-International Measurement Federation Secretariat; 2010. p. 412–21 [Google Scholar]
- N. Mole, G. Bobovnik, J. Kutin, B. Štok, I. Bajsić, Coupled fluid-structure simulation of the Coriolis flowmeter under forced vibration, in Soares BHVTaCAM, editor. Proceedings of the 10th International Conference on Civil, Structural and Environmental Engineering Computing (Civil-Comp Press, Scotland, 2004) [Google Scholar]
- C.P. Stack, T.J. Chunningham, Design and Analysis of Coriolis Mass Flowmeter using MSC_NASTRAN. http://webmscsoftwarecom/support/library/conf/wuc93/p05493pdf.1-17 [Google Scholar]
- V. Kumar, M. Anklin, Numerical simulation of coriolis flowmeters at low Reynolds number flows, J. Metrolog. Soc. India 26, 225–235 (2011) [Google Scholar]
- N. Mole, G. Bobovnik, J. Kutin, B. Štok, I. Bajsić, An improved three-dimensional coupled fluid-structure model for Coriolis flowmeters, J. Fluids Struct. 24, 559–575 (2008) [CrossRef] [Google Scholar]
- G. Bobovnik, N. Mole, J. Kutin, B. Štok, I. Bajsić, Coupled finite-volume/finite-element modelling of the straight-tube Coriolis flowmeter, J. Fluids Struct. 20, 785–800 (2005) [CrossRef] [Google Scholar]
- J.E. Smith, Method and structure for flow measurement. Google Patents; 1980 [Google Scholar]
- EF Management, Precision flow & density technology: Coriolis flowmeter K-factor calculation, 2014. http://www2emersonprocesscom/siteadmincenter/PM%20Micro%20Motion%20Documents/Flyer-K-Factor-14FA-MC-001949pdf [Google Scholar]
- M. Kazahaya, A mathematical model and error analysis of Coriolis mass flowmeters, IEEE Trans. Instru. Measur. 60, 1163–1174 (2011) [CrossRef] [Google Scholar]
- W. Merzkirch, K. Gersten, F. Peters, R.A.M.V. Vasanta, E. Von Lavante, V. Hans, Fluid mechanics of flow metering, 2005 [CrossRef] [Google Scholar]
- P. Tim, Understanding the Challenges of Two-Phase Flow, 2004. http://wwwemersoncom/resource/blob/66308/152c05189adf024662ad2aba500629de/understanding-the-challenges-of-two-phase-flow-datapdf [Google Scholar]
- A. Persson, The Coriolis Effect − a conflict between common sense and mathematics [Google Scholar]
- C. Clark, S. Wang, R. Cheesewright, The performance characteristics of a micro-machined Coriolis flow meter: an evaluation by simulation, Flow Measur. Instru. 17, 325–333 (2006) [CrossRef] [Google Scholar]
Cite this article as: Dalson Athanase Gace, On the performance of a Coriolis Mass Flowmeter (CMF): experimental measurement and FSI simulation, Int. J. Metrol. Qual. Eng. 13, 3 (2022)
All Tables
Dimensions (D1 to D6) and properties flow tubes: P1, P2, P3, P4, P5 and P6 are the density, Young modulus, thermal expansion, Poisson ratio, bulk and shear modulus, respectively.
Modal analysis: thirty-six possible modes corresponding to six degrees of freedom and six modal frequencies with corresponding amplitude ratios, r.
Mass measured by a CFM benchmarked to mass measured by a reference balance and corresponding measurement error for a CFM.
All Figures
 |
Fig. 1 CFD model of a U-shape tube: D1, D2, D3, D4, D5 are lengths of different sections of a CFM, D6 angle of bend of CFM pipe while A, B, C, D, E, F, G are key components on a CFM. The excitation, E is indicated by a yellow arrow in the z-direction. |
| In the text | |
 |
Fig. 2 Simulation chart: Model analysis and fluid flow coupled to tube oscillation iterative two-way fluid structure interactions. |
| In the text | |
 |
Fig. 3 Actual experimental setup of the entire flow system with U-shape CFM, reference balance, fluid stocking tanks, fluid channeling pipes, sensor and flow regulating valves. |
| In the text | |
 |
Fig. 4 Schematic experimental setup of the flow system indicating the main features like flow storage, flow measurements and flow regulators. T.I and P.I are the temperature indicator and pressure indicator, respectively. |
| In the text | |
 |
Fig. 5 Main experimental Procedures for measurements on a single phase fluid flow. PCP, ACo, CA, PA, DCS, LCV, GVF and NFR stand respectively for pump control panel, air compressor, air cylinder, pneumatic actuator, data communication system, gas volume fraction and nominal flowrate. |
| In the text | |
 |
Fig. 6 Mass computed flowrates for different grid resolutions and inlet velocities: (a) vin = 0.676 m/s, (b) vin = 3.382 m/s and vin = 8.117 m/s. |
| In the text | |
 |
Fig. 7 Proper mode of U-shape CFM corresponds to its oscillations at first natural frequency 93.467 Hz in z-directions. |
| In the text | |
 |
Fig. 8 Displacements of the tube oscillating under excitation force only. No flow flowing through the pipe. Displacement at sensor 1 and sensor 2 are plotted against time. |
| In the text | |
 |
Fig. 9 Displacements at sensor locations for the tube oscillating under excitation force and fluid flow through the pipe at a velocity of 7.305 m/s. |
| In the text | |
 |
Fig. 10 Variation of mass flowrates with time shifts between sensors. |
| In the text | |
 |
Fig. 11 Model validation: Mass computed mass flowrates plotted against measured mass flowrates for different values of the meter factor K. |
| In the text | |
 |
Fig. 12 Deviation between simulation results and measurements (green dots) evaluated against acceptable error limits. |
| In the text | |
 |
Fig. 13 Sensitivity of the CMF model computed with both a two way and a one-way FSIs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


