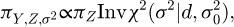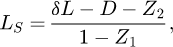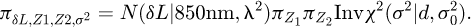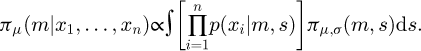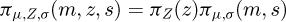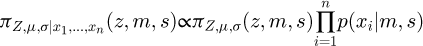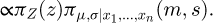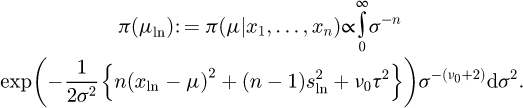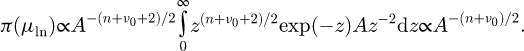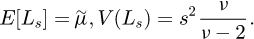| Issue |
Int. J. Metrol. Qual. Eng.
Volume 15, 2024
|
|
|---|---|---|
| Article Number | 14 | |
| Number of page(s) | 17 | |
| DOI | https://doi.org/10.1051/ijmqe/2024010 | |
| Published online | 13 August 2024 | |
Research article
Utilizing prior knowledge about the measurement process for uncertainty evaluation through plain Monte Carlo sampling
1
Physikalisch-Technische Bundesanstalt, Braunschweig and Berlin, Germany
2
Laboratoire National de Métrologie et d’Essais, 29 avenue Roger Hennequin, 78197 Trappes Cedex, France
* Corresponding author: manuel.marschall@ptb.de
Received:
14
March
2024
Accepted:
7
June
2024
Type A uncertainty evaluation can significantly benefit from incorporating prior knowledge about the precision of an employed measurement device, which allows for reliable uncertainty assessments with limited observations. The Bayesian framework, employing Bayes theorem and Markov Chain Monte Carlo (MCMC), is recommended to incorporate such prior knowledge in a statistically rigorous way. While MCMC is recommended, metrologists are usually well-familiar with plain Monte Carlo sampling and previous work demonstrated the integration of similar prior knowledge into an uncertainty evaluation framework following the plain Monte Carlo sampling of JCGM 101–the Supplement 1 to the GUM. In this work, we explore the potential and limitations of such an approach, presenting classes of data distributions for informative Type A uncertainty evaluations. Our work justifies an informative extension of the JCGM 101 Type A uncertainty evaluation from a statistical perspective, providing theoretical insight and practical guidance. Explicit distributions are proposed for input quantities in Type A scenarios, aligning with Bayesian uncertainty evaluations. In addition, inherent limitations of the JCGM 101 Monte Carlo approach are discussed concerning general Bayesian inference. Metrological examples support the theoretical findings, significantly expanding the applicability of the JCGM 101 Monte Carlo technique from a Bayesian perspective.
Key words: Bayesian uncertainty evaluation / Informative prior knowledge / Monte Carlo sampling / Markov Chain Monte Carlo
© M. Marschall et al., Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Uncertainty evaluation involving complex or non-linear models for univariate measurands is a common task in metrology. A well-known approach to obtain a state of knowledge distribution for the measurand based on plain Monte Carlo sampling is given in the document JCGM 101- the Supplement 1 to the Guide to the Expression of Uncertainty in Measurement (GUM) [1]. In this document, a probability density function (PDF) for the measurand is derived that “expresses the state of knowledge about the quantity, i.e., it quantifies the degree of belief about the values that can be assigned to the quantity based on the available information” [1, Introduction, p. vii]. The intention to provide state of knowledge distributions for a quantity is at the core of the Bayesian interpretation of probability and, according to Lindley, is “the only satisfactory description of uncertainty” [2].
The Bayesian paradigm is based on modelling one's knowledge about unknown quantities of a statistical model by using random variables, whose distributions are inferred by applying Bayes' rule to compute their so-called posterior distribution given available data. The posterior distribution depends on the likelihood function and a prior state of knowledge about the quantities. Choosing a prior makes it possible to reduce the resulting uncertainty by combining pure data with physical knowledge about the experiment or the quantities involved. Furthermore, a Bayesian inference enables probability statements, as well as the identification of credible intervals or conformity regions which are key elements and necessities in modern metrology.
Analytical formulas for the posterior that allow simple calculation of quantities of interest, such as the posterior mean or its variance, are rare. A widely applied, flexible, and powerful statistical technique to tackle this issue is Markov Chain Monte Carlo (MCMC) sampling [3]. While other alternative advanced MCMC approaches are also typically available in many statistical toolboxes, understanding their underlying principles and interpreting their results tends to require specialist statistical expertise. For more details on typical MCMC tools and their issues, cf. e.g. to [4] and the references therein. Plain Monte Carlo sampling, on the other hand, producing independent samples from a sought distribution. Moreover, it is a well-known technique in metrology. Having independent and identically distributed samples from the posterior would be the ideal scenario, which significantly simplifies computations and convergence assessments. Unfortunately, plain Monte Carlo sampling is not generally applicable for a Bayesian inference and a compromise between the complexity of the uncertainty evaluation approach and the simplicity of the numerical scheme may be sought. Therefore, it is of interest to explore the possibilities of a plain Monte Carlo approach in terms of its applicability in more general cases and where naive application of this procedure may fail to produce reasonable results.
In metrology, an uncertainty evaluation method based on plain Monte Carlo sampling is established in JCGM 101. The procedure outlined in that document is based on the propagation of distributions using Monte Carlo sampling. In particular, a model function for the measurand maps input quantities and their assigned state of knowledge distributions to the measurand and its corresponding state of knowledge distribution is obtained by Monte Carlo sampling. The resulting independent Monte Carlo samples of the distribution of the measurand can be used for statistical evaluation, e.g., to extract the mean and the standard deviation of its state of knowledge distribution, or coverage intervals. A crucial step in this approach is the definition of the distributions of the input quantities. Here, one typically distinguishes two cases: the presence of a series of observations (Type A) and the absence of observations but other knowledge (Type B). For the latter, JCGM 101 lists several examples and scenarios based, e.g., on the principle of maximum entropy [5]. While maximum entropy might be controversially discussed in the statistics community [6] and the inferred PDF from Type B information is a crucial ingredient for a successful uncertainty evaluation in metrology, the actual choice of this PDF is irrelevant for the procedure in this work. Likewise, expert elicitation [7,8] could be employed. In the presence of observations, the well-known Type A mechanism in JCGM-101 derives a PDF for the observed input quantity independently from all other quantities involved in the model for the measurand. Subsequently, independent samples are drawn from the joint distribution assigned to all input quantities and pushed forward through the model function for the measurand to obtain independent samples for the distribution of the measurand.
The assignment of a PDF for an input quantity by the Type A procedure in JCGM 101 is based on a specific Bayesian inference producing a state of knowledge distribution for the Type A input quantity. The question then arises whether the Monte Carlo sampling procedure is in line with a Bayesian inference. In particular, whether the resulting distribution for the measurand equals a posterior that would result from the application of Bayes theorem and the update of prior knowledge under the data observed. This question has fortunately been answered by several authors in the community [9–12]. The key argument is that the Type A uncertainty evaluation is based on a Bayesian inference using a noninformative prior for the parameter of the underlying Gaussian distribution for the data. Then, the subsequent PDF propagation through a model for the measurand results in a PDF that is equivalent to a Bayesian posterior with a specific joint prior. It is to note that, since the Bayesian posterior distribution coincides with the state of knowledge distribution derived by the concept of JCGM 101, coverage intervals are credible intervals.
This theoretical insight presents a justification for the approach recommended by the JCGM 101 from Bayesian point of view, cf. e.g., [13]. But, statisticians and metrologists might be dissatisfied with the specific choice of the prior, and also with the restriction to specific data distributions. Moreover, it has been shown that the automatic use of that prior leads to issues for low numbers of observations and can also lead to unsatisfactory or even poor results and challenges traceability [14–16]. From a practical perspective, O'Hagan and Cox [17] have shown and motivated that a simple informative Type A uncertainty evaluation is possible using an informative inverse χ2 prior for the variance of the data observed. The authors have shown that using this flexible prior in a Type A uncertainty evaluation results in a scaled and shifted t-distribution, that itself is the result of a Bayesian inference. This distribution can then be used in a Monte Carlo propagation of distributions for an arbitrary model for the measurand. In another work [18, Section 9] Meija et al. generalize this algorithmic proceeding to include more general prior knowledge, which ultimately requires the use of MCMC.
In this work, we derive a theoretical framework that justifies the procedure of [17] and [18, Section 9] from a theoretical point of view, cf. Figure 1. Moreover, we give practical examples, extending [17], where plain Monte Carlo sampling can be applied instead of sophisticated sampling techniques. By restricting the class of potential prior distributions and data distributions, we implement the procedure of [18, Section 9] by Monte Carlo techniques, without the need to use MCMC. In this way, we extend the concept of Type A uncertainty evaluation to the general class of location-scale distributions for which an informative prior for the variance of the data can be employed in a simple way. We show that the subsequent propagation of distributions, as advocated by JCGM 101, can be used to obtain a PDF that would result from a Bayesian inference using a specific prior for the measurand and all unknowns involved. This prior admits important properties that are natural requirements in metrology, e.g., that it produces a posterior for Type B quantities that is unaffected by the data. These results lead to a significant extension of the Type A uncertainty evaluation procedure and the applicability of the Monte Carlo technique of JCGM 101 from a Bayesian perspective and allows to extend JCGM 101 to include meaningful prior knowledge about the precision of a employed measurement device into its analysis.
Numerical examples from metrological applications underpin our theoretical findings, and they highlight the adequacy of the informative Type A uncertainty evaluation with subsequent propagation of distributions in comparison to a conventional Bayesian approach. Beside theoretical justification and numerical feasibility, we also explore the limitations of the approach proposed.
A graphical representation of our contributions is given in Figure 1 and the organisation of the manuscript is as follows. In Section 2, the theoretical framework for a rigorous Bayesian inference using informative prior knowledge is derived. Then, the comparison to an informative Type A uncertainty evaluation of an input quantity with subsequent propagation through a model for the measurand is performed. Section 3 presents practical examples by giving explicit Type A PDF assignment strategies that extend the current state of the art in JCGM 101. In Section 4, an example is presented that does not fall into the category of location-scale distributions. Some conclusions are finally given in Section 5.
 |
Fig. 1 Graphical abstract for the methodology and contributions in this work. Informative Bayesian Type A uncertainty evaluation and subsequent Monte Carlo propagation to obtain a state of knowledge distribution for the measurand is presented. If independent sampling from the marginal posterior πμ(m|x1, … , xm), cf. (1), is possible, plain Monte Carlo sampling can be used to sample from the posterior distribution for the measurand by combining samples from πμ(m|x1, … , xn) with samples from the Type B state of knowledge PDF πZ (z). The theoretical justification is given in Section 2 and practical examples are given in Section 3. |
2 Bridging an informative approach following JCGM 101 and conventional Bayesian inference for location-scale data distributions
Deriving a state of knowledge distribution for the measurand is a common task in metrology and the possibility to include prior knowledge is desired, particularly for a low number of observations. Informative Type A uncertainty evaluation is a possible methodology to achieve this goal. This section is devoted to a short introduction of this approach for general location-scale data distributions, its requirements for practical applications, and the use of plain Monte Carlo sampling to obtain the PDF for the measurand desired. Subsequently, this proceeding is embedded in a Bayesian framework, to bridge the informative Type A uncertainty evaluation to a conventional Bayesian inference applied directly for the measurand.
2.1 Informative Type A uncertainty evaluation for location-scale data distributions
In this section, an informative Type A uncertainy evaluation procedure is derived, assuming a general location-scale data distribution for a set of observations. A location-scale distribution is a probability distribution that is parametrised by a location parameter and a scale parameter, here and further denoted as μ and σ respectively. Well-known examples are the Gaussian distribution with mean μ and standard deviation σ, and the scaled and shifted t-distribution for any number of degrees of freedom. For an introduction to location-scale distributions, we refer to [19].
Distributions of the location-scale type are frequently used in statistics to describe the distribution of data observed [20]. In metrology, location-scale distributions have a natural interpretation, where the location parameter can represent the quantity for which Type A information is present and the scale parameter reflects the spread of the data distribution. The latter results, e.g., from the fluctuations arising during the measurement.
In the case of Type A information, observations are available that can reasonably be modelled by some distribution. Considering a distribution from the location-scale family, an inference for μ and σ has to be performed. In metrology and particularly in JCGM 101 clause 6.4.9.2, a Type A uncertainty evaluation is based on the assumption that the recordings are normally distributed and a Bayesian inference is performed. This inference employs flat priors for the location and for the logarithm of the scale parameter. The resulting marginal posterior PDF of the location parameter is then taken as PDF derived by the Type A formalism. As discussed earlier, this choice is subject to debates in the community.
In this section, we generalize this approach. On the one hand to more general location-scale distributions allowing metrologists a more flexible and probabilistic modelling of observations. On the other hand, to allow metrologists to include prior knowledge about the scale parameter, e.g., arising from prior knowledge of their measurement device. For this, let x1, … , xn denote independent and univariate recordings of a quantity X that follow a location-scale distribution with unknown location μ ∈ ℝ and unknown scale σ > 0. The quantity X is assumed to equal the location parameter μ of the distribution, so that the marginal posterior for μ will be assigned as the PDF for X. In some cases, however, X can be a function of both, location μ and scale σ, as for the lognormal distribution in Section 3.2. In that case the joint posterior for μ and σ is propagated through that function to yield the PDF for X.
Denote by πμ,σ the joint prior distribution for the location and scale parameter. Then, the marginal posterior1 PDF for the location parameter is given by
where  denotes the likelihood function induced by the location-scale distribution. In the following, we assume that the PDF (1) is well-defined.
denotes the likelihood function induced by the location-scale distribution. In the following, we assume that the PDF (1) is well-defined.
Example 1 Assume the recordings x1,...xn are drawn independently from a normal distribution with unknown mean μ and unknown variance σ2. Employing the prior  , which assigns a noninformative (flat) prior to the mean and an inverse Gamma prior with shape parameter a >0 and scale parameter b > 0 to the variance. Then, the resulting marginal posterior for the mean is a scaled and shifted t-distribution with n + 2a - 1 degrees of freedom, shifted by the mean of the data observed and scaled by
, which assigns a noninformative (flat) prior to the mean and an inverse Gamma prior with shape parameter a >0 and scale parameter b > 0 to the variance. Then, the resulting marginal posterior for the mean is a scaled and shifted t-distribution with n + 2a - 1 degrees of freedom, shifted by the mean of the data observed and scaled by  , where s denotes the empirical standard deviation of the data observed. The resulting PDF is proper, even for n=1 and all choices of a,b > 0. However, the PDF has no mean value if n + 2a < 2. For a careful discussion on the choice of the parameter a and b given prior knowledge about the measurement device, cf.
[21].
, where s denotes the empirical standard deviation of the data observed. The resulting PDF is proper, even for n=1 and all choices of a,b > 0. However, the PDF has no mean value if n + 2a < 2. For a careful discussion on the choice of the parameter a and b given prior knowledge about the measurement device, cf.
[21].
2.2 Deriving a state of knowledge distribution for the measurand
In the following, consider a general model for the measurand of the form
In this work, the measurand Y is assumed to be univariate, just as the quantity X for which independent recordings x1,...,xn are available. As considered above, assume that X follows a location-scale distribution with unknown real-valued location parameter μ and unknown scale parameter σ > 0. The quantity Z may be multivariate and π(z) denotes an available state of knowledge distribution of Z with Type B information. We like to point out that the actual properties of the PDF assigned to Z are crucial for a successful uncertainty evaluation in metrological applications. However, whether this PDF is derived using expert elicitation, a maximum likelihood or Bayesian inference, or the application of the maximum entropy principle plays no role for the upcoming procedure.
In this work, we explicitly highlight the case of having a quantity X with Type A information and a set of parameters Z with Type B information. While the JCGM 101 usually summarizes these quantities and only considers their joint PDF for the propagation of distributions, the previously introduced treatment of informative Type A uncertainty evaluation requires this distinction. In practical terms and referring to the mass calibration example in Section 3.1, the quantity X may correspond to a set of repeated but independent recordings of a mass difference between a reference standard and some unknown mass. The parameters in Z additionally influence the measurement of the unknown mass and, e.g., correspond to the conventional mass of the reference standard, the drift of its value, a correction for eccentricity and the magnetic effects and a correction for air buoyancy [22].
In the following, we will derive two approaches to obtain a state of knowledge distribution for the measurand Y given prior knowledge about the variance of the data σ2. In Section 2.2.1, a procedure is introduced that is based on the concepts of JCGM 101. In particular, we present a propagation of distributions approach that can in many cases be tackled by plain Monte Carlo sampling. In Section 2.2.2, a fully Bayesian approach to estimate the posterior PDF for the measurand is performed. This approach also allows to include prior knowledge about the measurand Y. Subsequently, in Section 2.3, both approaches are related and a theoretical justification for the propagation of distributions approach from a Bayesian perspective is presented.
2.2.1 Informative Type A uncertainty evaluation and propagation of distributions
JCGM 101 presents a Monte Carlo sampling procedure that is used for the propagation of distributions. Using the notation from the previous sections, a state of knowledge distribution is assigned to X. In JCGM 101, this is done by assigning the marginal posterior for μ, i.e., the mean of the data distribution assumed, from (1) to X where the prior πμ,σ (m, s) ∝ 1/s is used. Here and in the following, the prior πμ,σ is no longer restricted to the specific prior used in JCGM 101 and X can be some function of μ, such that the distribution of X might be obtained by Monte Carlo sampling using the marginal posterior for μ as input distribution. This distribution of X is then combined independently with the state of knowledge distribution for Z. Subsequently a propagation of distributions can be performed for the input quantities X and Z through the model function f for the measurand (2). In this way, application of the Monte Carlo method will produce independent samples from the distribution of the measurand. Then, the resulting large sample for the measurand Y can be used for uncertainty quantification, e.g., to compute an estimate, a standard uncertainty or coverage intervals. For future reference, the resulting distribution for the measurand from this propagation of distributions approach will be called πY.
The informative Type A uncertainty evaluation procedure can be summarized using the following three steps:
Assign a data distribution depending on the location μ and scale σ to the recordings x1,...,xn and translate the knowledge of the measurement instrument in a prior for μ and σ.
Generate samples from the marginal posterior (1) and optionally propagate these samples to obtain samples from the PDF of the quantity X.
Combine the samples from step two independently with samples of the PDF of Z and propagate them through the model for the measurand (2) using the Monte Carlo procedure of JCGM 101.
While the third step is well-known from available guidance documents, steps one and two require some additional explanation to ensure practical applicability beyond the choice in Example 1. Therefore, Section 3 demonstrates in terms of practical examples how to apply this procedure. We also refer again to [17] for explicit guidance on the case of normally distributed observations and prior knowledge about the variance of the data distribution, which can be extracted from knowledge about the measurement instrument. We like to point out that our approach presented above is not limited to the noninformative prior for μ taken in [17]. Our only requirement is that one is able to sample efficiently from the marginal posterior (1). Taking a flat prior for μ here can be seen as a mathematical convenience to obtain simple formulas. Replacing the improper prior with a proper but vaguely informative prior with large variance yields numerically the same posterior.
The remainder of this section is concerned with a theoretical assessment of the procedure described above. In particular, we will show that the resulting PDF for the measurand can be justified from a statistical point-of-view in that it equals a marginal posterior from a conventional Bayesian inference using a specific prior. Readers concerned with the practical implications of this approach are refereed to Section 3.
2.2.2 Bayesian inference directly for the measurand
From a statistical perspective, it is more natural to apply Bayes theorem directly to the measurand instead of the parameters of the data distribution. For this, it is important to assume that the model function for the measurand f in (2) is partially invertible in the sense that there exists a unique observation model function g that takes the measurand as input and has the observed quantity X as output
This assumption is, on the one hand, crucial to allow a Bayesian inference to be performed in the parameterisation given by (θ,Y,Z) where θ denote further parameters of the data distribution for the recordings x1,...,xn such as its variance σ2. On the other hand, the assumption is not severely restrictive, since models for the measurand are usually of a simple form, or already given by an inverse problem involving the observation model function. A general class of partially invertible models for the measurand and their Bayesian treatment is presented in [23].
The Bayesian procedure requires to assign a prior to all unknowns πY,Z,σ. The resulting marginal posterior for the measurand reads
For the definition and existence of the posterior PDF we refer to the literature [24,25]. We assume in the following that the PDF (4) is well-defined.
2.3 Connection and theoretical justification
The main goal of this work is to establish a generalized Type A inference, that can be used in a Monte Carlo propagation scheme to generate a PDF for the measurand, and that is equivalent to a marginal posterior arising in a conventional Bayesian inference. The following theorem collects the important ingredients.
Theorem 1 Assume that there exists an observation model function (3) that is the partial inverse of the model for the measurand (2). The informative Type A uncertainty evaluation approach assigns2 to X the marginal posterior for μ from (1). Assuming this PDF exists, this PDF can be combined with the state of knowledge PDF for Z by taking the product of both PDFs as the joint PDF. Then, propagation through the model of the measurand (2) results in the PDF πY for the measurand. Assuming the observation model function g of (3) is continuously differentiable with respect to y, the PDF πY is equivalent to the marginal posterior for the measurand (4), where the joint prior
has been used for the Bayesian inference.
The proof is given in Appendix A. Some immediate consequences of this Theorem are given in the following.
Corollary 1 Given the same assumptions as in Theorem 1, a Type A uncertainty evaluation with subsequent propagation of distributions is equivalent to a Bayesian inference for the measurand if the Type A uncertainty evaluation is itself the result of a Bayesian inference. Moreover, coverage intervals that are obtained from the resulting distribution for the measurand are credible intervals.
Example 2 For the class of GUM measurement models considered in [23] , reformulated here as Y = C (Z) X + G (Z) where C and G are smooth functions of Z (C (Z)#0), observe that
Assuming a flat prior for μ, Theorem (1) gives the expression of the prior distribution  for which the informative Type A Monte Carlo approach and the fully Bayesian approach are equivalent
for which the informative Type A Monte Carlo approach and the fully Bayesian approach are equivalent
with this prior and assuming independent and identical normally distributed observations xi|μ, σ2 ∼ N (μ, σ2) , i = 1, … , n, the posterior distribution marginalized over the variance parameter writes
Applying the change of variables Y→μ yields
where  .
.
As a result,  can be factorized as
can be factorized as
with πZ(z|x1, … , xn) = πZ (z) so that the informative Type A and the Type B can be sampled independently in a subsequent Monte Carlo approach.
For this example, assuming a constant prior for the logarithm of the variance  , the corresponding distribution assigned to the quantity X with Type A information is given by
, the corresponding distribution assigned to the quantity X with Type A information is given by
which is the classical result in JCGM 101 for modelling Type A uncertainty from a series of n independent observations with unknown variance.
Another important result that can be derived from the theorem above is given in the following corollary. In particular, knowledge about a quantity with Type B information is not affected by recordings of another quantity corresponding to Type A information. It can easily be shown (see Appendix A) that the prior presented in Theorem 1 results in a joint posterior that fulfills this property.
Corollary 2 Given the same assumptions as in Theorem 1, the specific structure of the prior underlying the JCGM 101 analysis implies that the marginal posterior for the quantity Z with Type B information always equals its prior. In particular it holds  .
.
We like to mention that location-scale distributions serve as a prototype for classes of distributions for which the theory derived holds. Distributions with a location and a scale parameter are natural choices in a metrological context and might be understood similarly to a Gaussian distribution. However, the reasoning above holds for more general classes of distributions and we will later explore examples that do not fit in the location-scale category. In particular, the discrete Poisson distribution will be treated in Example 4, which is a one parameter distribution. Moreover, the theoretical considerations can be generalized to the multivariate case, i.e., having vector-valued observations and hence a multivariate prior distribution assigned to the quantity X. The treatment of this case, including the usage of correlations, is generally possible but is out of scope for this work.
2.4 Discussion
The final result of this section, Theorem 1, gives the formal justification from a Bayesian perspective for the concept of informative Type A uncertainty evaluation procedures on input quantities with subsequent propagation of distributions through a model for the measurand. It is important to note that, the conceptual difference between a Type A uncertainty evaluation with a subsequent propagation of distributions and a direct Bayesian approach for the measurand, lies in the different parametrisations considered and the specific structure of the prior underlying JCGM 101. The former considers the variables (μ,σ,Z) as the parameters of inference and performs Monte Carlo sampling to obtain the distribution of the measurand Y, whereas the latter directly considers the variables (Y, σ, Z). Obviously, it is possible to compare the two approaches only if there is a one-to-one relation between the parameterisations. Then, the equivalence follows directly from the consistency of probability calculus. Assuming only a local invertibility of the model for the measurand is not sufficient.
The theoretical considerations above hold for arbitrary prior distributions, as long as some weak regularity and integrability assumptions ensure the existence of the involved PDFs. In practice, a prior needs to be assigned either in terms of (Y, σ, Z) or in (μ,σ,Z), depending on the parametrisation chosen. This prior is able to reflect all expert knowledge about the involved quantities. For the instrument accuracy, or equivalently for the variance of the data distribution σ2, this might be the assumption that the spread of the data has a high probability to be within a certain range. The precarious part of the prior assignment lies in the consideration of the measurand Y and the location parameter μ. We have shown previously that, assigning any prior for μ, jointly with Z and σ, can be translated to a Bayesian procedure in the parametrisation (Y, σ, Z). The key result of this paper is that among all potential priors for (Y, σ, Z), the prior derived in Theorem 1 is the one that ensures the compatibility with an informative Type A JCGM 101 procedure, which implies the following key feature: it makes the quantities corresponding to Type A and Type B information (a priori) independent as stated in Corollary 2 and shown in the proof of Theorem 1, cf. Appendix A. This is an immediate consequence of the structure of the prior chosen which factorizes into the prior for the Type B variables Z and a prior for the parameters μ and σ of the data distribution. Whether such a restrictive assumption about the prior can be deemed appropriate depends on the particular application. In any case, it lacks the flexibility of a conventional Bayesian inference in which the prior is chosen to reflect one's particular prior knowledge about the application considered.
As expected from its construction, the direct Bayesian approach given by Theorem 1 shares the same limitations as the JCGM 101 uncertainty evaluations, e.g., when it comes to encompass physically meaningful prior knowledge on the measurand. Treating the quantities with Type A and Type B information independently can result in non-physical prior knowledge for Y. The reason for that is the inherent dependency of μ and Z (when treating Y and Z as independent, cf. [16]), due to the model for the observations and that this dependency cannot be adequately modeled by the approach followed in JCGM 101. This limitation can generally not be alleviated by performing informative Type A uncertainty evaluation [16]. Hence, the informative approach for the JCGM 101 procedure presented may also challenge transferability [15] and long-run success rate [14]. Moreover, Theorem 1 directly implies and shows the well-known effect that prior ignorance in one parametrisation does not equal prior ignorance in the other parametrisation or vice versa. This means, particularly for non-linear models for the measurand, that the modelling of a noninformative prior for the location parameter μ, does not equal a noninformative prior for the measurand. The effect of this observation will be discussed in Section 3.2. Metrologists should be aware of this issue and corresponding guidance, also with input from a statistical perspective, are required to ensure safe applicability of these approaches.
At this point it is also to note that in some complex situations, such as the solution of dynamical systems or differential equations, the partial inverse mapping g might not be accessible. In these cases one might argue that the informative Type A uncertainty evaluation approach of Section 2.1 can be applied anyway to the model function for the measurand f, since only the state of knowledge distributions for the quantities X and Z are required. While this is possible in practice and the propagation of state of knowledge distributions through the function f reflects also a state of knowledge about the measurand, the important theoretical justification, in terms of the equivalence to a Bayesian marginal posterior, is not longer available. This includes the equivalence in Corollary 1 between coverage and credible intervals.
Another important aspect that is not covered by the theoretical assessment above is the complexity of the involved computations. Theorem 1 states that the marginal Bayes posterior of the Type A uncertainty evaluation πμ has to be combined with the state of knowledge distribution πZ. In practice, this is not always a trivial task. For example, when there is no analytical representation for the marginal posterior πμ, drawing samples might not be straightforward. These scenarios can, however, still be tackled using techniques like MCMC or Monte Carlo rejection sampling. In the following examples of Section 3 and Section 4, we focus on the practical implications of the procedure derived and present scenarios in which a plain Monte Carlo propagation can be performed.
3 Examples for location-scale data distributions
In this section, we want to motivate different choices of informative Type A uncertainty evaluation scenarios. In particular, some data distributions and corresponding prior knowledge are discussed, for which analytical marginal posterior distributions are produced and plain Monte Carlo sampling can be applied to end up with a posterior distribution. Additionally, we give practical considerations for each setting and refer practitioners to the underlying assumptions and implications. As a reference procedure for comparison, we include for each example a direct Bayesian treatment using a prior which expresses vagueness about the measurand (rather than about the Type A input quantity), which we call conventional Bayesian in the following. It is important to note that, the prior chosen for the conventional Bayesian approach does in general not coincide with the prior derived in Theorem 1. However, this choice highlights the conceptual difference between choosing a vague prior for the measurand and the theoretical prior derived above.
3.1 Normal distributed observations
This classical situation is often assumed in metrology and already covered in JCGM 101. In particular, we assume n ≥ 1 independent observations of a quantity μ having Gaussian measurement errors with standard deviation σ.
The example considered here is taken from [21], which adjusted example S2 from the EA-4/02 uncertainty guideline [22] and it deals with the calibration of a weight of mass 10 kg. The linear model for the measurand mX reads
where δm denotes the observed mass difference to a reference standard and mX is the unknown mass. The quantity Z collects multiple influences and is given by the sum of four quantities, to which the following distributions are assigned: a normal distribution with mean 5 mg and standard deviation 22.5 mg, two rectangular distributions over the interval [-10 mg, 10 mg] and a rectangular distribution over the interval [-15 mg, 15 mg]. For details, we refer to [22]. The observations for the mass difference δm are 10 mg, 30 mg and 20 mg. The factor α= 0.1 is introduced here to reduce the impact of Z on the resulting estimate and uncertainty for the measurand mX, i.e., to increase the uncertainty induced by the observed quantity. For the standard deviation of the distribution of the data σ0 = 25 mg is taken, cf. [21].
3.1.1 JCGM 101 Type A uncertainty evaluation without prior knowledge
The JCGM 101 considers in [1, clause 6.4.9.2] a Bayesian procedure to obtain a state of knowledge PDF for the mean of a normal distribution μ by assigning the joint noninformative prior (NIP)  . The resulting marginal posterior for μ is a t-distribution with n-1 degrees of freedom, shifted to the empirical mean of the observations and scaled by the empirical standard deviation divided by
. The resulting marginal posterior for μ is a t-distribution with n-1 degrees of freedom, shifted to the empirical mean of the observations and scaled by the empirical standard deviation divided by  . This distribution can now be assigned to the quantity δm and a Monte Carlo propagation can be performed to obtain a state of knowledge distribution for the measurand mX. This approach will be denoted NIP for noninformative prior in the following.
. This distribution can now be assigned to the quantity δm and a Monte Carlo propagation can be performed to obtain a state of knowledge distribution for the measurand mX. This approach will be denoted NIP for noninformative prior in the following.
Note that we do not consider the case of perfect prior knowledge about σ here, i.e., the information about the estimate σ0 is not used for this approach. For a discussion on the use of σ0, assuming no remaining variability for the variance of the data distribution and subsequently assigning a normal distribution to δm, we refer to the example compendium [26]
3.1.2 Informative Type A uncertainty evaluation
A sensible choice for a joint partially informative prior for μ and σ is considered in [17]. In this work, no information about the location parameter is considered, but the scale parameter, here identified by the variance of the distribution of the data σ2 that reflects the precision of the measurement instrument, is assigned an inverse χ2 distribution. This means, one assumes
where σ0 is some estimate for the standard deviation of the data variability and d is set to either d=3 for a mildly informative prior (MIP) and to d=8 for a strongly informative prior (SIP). For details on the interpretation and reasoning of these choices, we refer to [17]. The resulting marginal posterior for the location parameter μ is again a scaled and shifted t-distribution with n- 1+ d degrees of freedom, shifted to the empirical mean of the data observed and scaled by the pooled standard deviation  , where
, where  denotes the empirical standard deviation of the data. This PDF, representing a state of knowledge distribution for the quantity δm with Type A information, can now be employed in a subsequent Monte Carlo propagation using the model for the measurand, just as in the NIP approach. Again, we like to point out that the choice of the improper noninformative prior for the location parameter is taken for mathematical convenience. Considering a proper, but vague, prior with large variance for μ in (13) yields numerically the same marginal posterior.
denotes the empirical standard deviation of the data. This PDF, representing a state of knowledge distribution for the quantity δm with Type A information, can now be employed in a subsequent Monte Carlo propagation using the model for the measurand, just as in the NIP approach. Again, we like to point out that the choice of the improper noninformative prior for the location parameter is taken for mathematical convenience. Considering a proper, but vague, prior with large variance for μ in (13) yields numerically the same marginal posterior.
With this choice of prior information, Theorem 1 gives an explicit formula for the induced prior for the measurand. Using the linearity of this model, it follows
which corresponds to the choice of a flat prior for the measurand. Taking this joint prior for a Bayesian inference for the measurand, yields therefore the same PDF as the informative Type A uncertainty evaluation with subsequent Monte Carlo propagation. The resulting PDFs for the measurand will be denoted MIP (MC) and SIP (MC), respectively.
3.1.3 Conventional Bayesian approach
We briefly provide a direct Bayesian approach to the problem of deriving a state of knowledge PDF for the measurand mX using the model function for the observations δm = mX − αZ. This requires the assignment of a prior PDF to the measurand mX, jointly with the parameter Z and σ. It might be reasonable to assign a Gaussian prior to the measurand, centered at 0 and with some large variance λ2. For the variance of the data, again an informative prior can be assigned in terms of an inverse χ2 distribution with d =3 (MIP) or d =8 (SIP). The resulting joint prior reads
The parameter λ steers the influence of the prior for the measurand. We consider a rather large value λ=103 mg, which reduces the information imposed by the measurand prior and the measurand prior appears almost flat. Sampling from the posterior can usually not be tackled with plain Monte Carlo, opposed to the direct Bayesian approaches, including prior knowledge for the measurand, described above. Alternatives that require additional knowledge are, e.g., MCMC, the simple Bayes approach using inverse transform sampling from [21], the explicit integration in [27] and the rejection sampling approach of [16]. In the following numerical computations, we employ MCMC to generate samples from the marginal posterior for the measurand and consider again the values d = 3 for a mildly informative prior for the variance and d = 8 for a strongly informative prior for the variance. Analogously, we will denote the resulting posterior PDFs for the measurand as MIP (MCMC) and SIP (MCMC).
3.1.4 Results and discussion
In Figure 2 we show the resulting state of knowledge distributions for the measurand arising from the different modelling approaches discussed. The blue line corresponds to the NIP approach, which makes implicit use of a noninformative prior for the location and scale parameter (μ, σ). The green and red solid lines are PDFs for the measurand, for which prior knowledge regarding the scale parameter σ is employed, but no information about the location parameter is assumed. Moreover, these PDFs are estimated using plain Monte Carlo and no sophisticated sampling procedure was required. The dotted lines correspond to posterior PDFs that arise when applying the conventional Bayesian approach, assuming the same prior for the scale parameter and a vague prior for the measurand. These posterior PDFs have been computed using the python MCMC library emcee [28] and all PDFs shown in this work are normalized to unity. It can be seen that the informative Type A uncertainty evaluation procedures (solid lines), employing plain Monte Carlo only, result in identical PDFs as the conventional Bayesian computations using MCMC. To underpin this claim, Table 1 quantitatively shows the similarity of the approaches in terms of the resulting estimates, the standard deviation of the PDFs, and 95% coverage intervals. This observation is also backed by the theoretical justification of Section 2, since the prior for the measurand induced by the flat prior for μ and Theorem 1 has to be flat. This means, when performing an informative Type A uncertainty evaluation with subsequent Monte Carlo propagation as above, the metrologist ignores prior knowledge about the Type A quantity μ. On the other hand, when assuming an almost flat prior for the measurand, the metrologist ignores prior knowledge about the measurand Y. In the present case, having a linear model for the measurand (12) and flat priors for the measurand and location parameter, Theorem 1 guarantees equivalence of both approaches.
The numeric values given in Table 1 are subject to variability due to the numerical computations employed. The mean has been constant for all procedures. However, the standard deviation fluctuates, especially for the MCMC computations, even when considering the large sample size. Therefore, we repeated the computations three times. The Monte Carlo (MC) computations used 108 samples each and we obtained for the standard uncertainty of the MIP (MC) and SIP (MC) approach a fluctuation smaller than the digits shown in Table 1. The MCMC computations considered 64 parallel chains, each generating 106 samples and a burn-in of 2000 samples was considered. The resulting standard uncertainty for the three repetitions are observed as [15.40,15.39,15.37] for the MIP (MCMC) and [14.95,14.94,14.94] for the SIP (MCMC) case. To achieve this stability, the MCMC computations using a standard (but state-of-the-art) Metropolis-Hastings algorithm required a total of 64 million samples, which took about 2.5 hours. In comparison, the MC methods, sampling from the exact same PDF, took only seconds.
We like to note that the PDF obtained by the NIP approach has no finite variance, i.e. the standard uncertainty of the PDF is not defined. We indicate this by the symbol ∞, which can be justified by taking an arbitrary series of finite domains of integration, which grow in volume. The standard deviation estimated on these domains diverges as the volume of the domains approaches infinity. Moreover, the coverage intervals obtained by the NIP are significantly smaller than those obtained by the approaches that additionally consider prior knowledge. The reason for that is the small number of observations and the fact that the estimation procedure of the NIP underrates the uncertainty. The approaches using informative prior knowledge are, on the other hand, more reliable.
 |
Fig. 2 Results for the example of Section 3.1. We show the resulting state of knowledge distribution for the measurand mX, denoting the deviation of a weight of mass 10 kg. We show the PDFs resulting using the noninformative prior (NIP) in blue, the mildly informative prior (MIP) in green and the strongly informative prior (SIP) in red. Both, MIP and SIP, are computed once using plain Monte Carlo (MC) and once using a vague prior for the measurand and MCMC. |
Statistical assessment of the resulting PDFs with values given in mg. From left to right we collect the mean estimate, the standard uncertainty given by the standard deviation of the PDF, and a 95% coverage interval. Also, the total number of samples generated and the corresponding computation is time is shown. The standard deviation of the measurand for the NIP approach is not defined, since only three measurements are present.
3.2 Lognormal distributed observations
Several applications in metrology deal with inherently positive observable quantities. For instance [29] considers electric field measurements of coupled biconical antennas in a screened room. Also [30] argues that many concentrations of measured substances admit data distributions that follow a lognormal distribution. Those measurements tend to have non symmetrical deviations from a nominal value towards one side, whereas taking the logarithm of the observations reveals a typical Gaussian behaviour. Such a situation can be modeled using a lognormal distribution. To this end, the logarithm of the observation is assumed to deviate from a location parameter or nominal value μ by Gaussian errors having standard deviation σ. In formulae, independent observations x1,...,xn follow a lognormal distribution with parameter μ and σ if
In the case of lognormal observations, the interpretation of both parameters μ and σ is different than under the Gaussian assumption. In particular, the location parameter μ is not the mean of the lognormal sampling distribution, which is given by exp(μ + σ2/2) and its standard deviation is given by  . However, similar uncertainty evaluation approaches based on different levels of information available for μ and σ, can be employed.
. However, similar uncertainty evaluation approaches based on different levels of information available for μ and σ, can be employed.
For the purpose of illustration we take inspiration from the gauge block calibration example [1, clause 9.5, Eq. (37)] and modify it to fit the scenario described above. The considered model for the measurand, i.e., the deviation δL of the considered gauge block to a nominal length is given by
The measured deviations D from a reference gauge block are estimated from Type A information. Following the example, a t-distribution with 24 degrees of freedom, a mean of 215 nm, and a standard deviation of 6 nm is derived for the state of knowledge distribution of D and fixed for this example. Type B information are available for Z1 and Z2 in [1, Table 10]. Deviating from the example in the guide, we consider LS as another quantity for which Type A information are available. In particular, we assume that there are 10 calibration measurements available for LS, as given in Table C1. Since these measurements represent a positive length, we generated them from a lognormal distribution that admits the same mean and variance as the t-distribution that was assigned to LS in [1, Table 10]. The derivation of the true parameter μ* and σ* used to generate the measurements and the actual simulated measurements considered are given in Appendix C. These recordings are now assumed to follow a lognormal distribution with unknown location parameter μ and unknown scale parameter σ. Then, similar noninformative and informative Type A PDF uncertainty evaluation procedures can be applied, as in the case with normal distributed observations. Subsequently, a state of knowledge PDF derived for μ can be used in a plain Monte Carlo propagation to obtain the distribution of LS = exp(μ), which assigns the median of the lognormal distribution to the quantity with Type A information.
3.2.1 JCGM 101 Type A uncertainty evaluation without prior knowledge
The JCGM 101 does not consider the case of lognormal observations. However, an analogous procedure as for Gaussian observations can be derived using a Bayesian inference for the parameters in (16). To this end, the noninformative prior πμ,σ (m, s) ∝ 1/s is considered in conjunction with the independent recordings x1,...,xn. The resulting marginal posterior for μ is a t-distribution with n-1 degrees of freedom, shifted to the mean 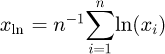 and scaled by
and scaled by 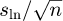 with
with 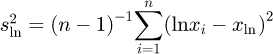 . In a second step, this PDF is propagated to LS = exp(μ) using plain Monte Carlo sampling and subsequently combined with the PDFs for the remaining quantities of the model for the measurand, to obtain a PDF for the measurand δL.
. In a second step, this PDF is propagated to LS = exp(μ) using plain Monte Carlo sampling and subsequently combined with the PDFs for the remaining quantities of the model for the measurand, to obtain a PDF for the measurand δL.
Due to the similarity with the case of normally distributed data, we will denote this approach also NIP in the numerical comparison.
3.2.2 Informative Type A uncertainty evaluation
Similarly as in the case of Gaussian observations, an informative prior can be employed for the unknown parameters μ and σ. In particular, a noninformative flat prior can be assigned to μ to not impose any prior knowledge about the location. For the scale, an  prior can again be used for the parameter σ2 to model prior knowledge about the variability of the distribution of the data. The resulting marginal posterior for the location parameter μ is again a t-distribution with n–1+d degrees of freedom, shifted by the mean
prior can again be used for the parameter σ2 to model prior knowledge about the variability of the distribution of the data. The resulting marginal posterior for the location parameter μ is again a t-distribution with n–1+d degrees of freedom, shifted by the mean 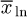 and scaled by
and scaled by  . A detailed derivation can be found in Appendix B. Analogously to the JCGM 101 approach, a PDF for the measurand δL can be obtained using plain Monte Carlo sampling.
. A detailed derivation can be found in Appendix B. Analogously to the JCGM 101 approach, a PDF for the measurand δL can be obtained using plain Monte Carlo sampling.
To actually incorporate prior knowledge, we also require a guess for the scale parameter σ0 and the elicitation process from the previous example can not be applied anymore, due to the different interpretation of σ. When dealing with lognormal observations, one might have access to the half length of a 95% coverage interval of the coefficient of variation, which describes the spread of the quotient of standard deviation and mean of the distribution of the recordings. For the lognormal distribution, the coefficient of variation is given by  . From this, we are able to numerically estimate the value for σ0, such that samples drawn from the corresponding
. From this, we are able to numerically estimate the value for σ0, such that samples drawn from the corresponding  distribution generate the half width of a 95 % coverage interval of c(σ) that corresponds to an assumed half-length. For the example here, we assume the half-length of a 95% coverage interval for the coefficient of variation is given by U95 = 500 nm. This assumption results in the a priori guess σ0 = 3.625 × 10−8 in a.u.
distribution generate the half width of a 95 % coverage interval of c(σ) that corresponds to an assumed half-length. For the example here, we assume the half-length of a 95% coverage interval for the coefficient of variation is given by U95 = 500 nm. This assumption results in the a priori guess σ0 = 3.625 × 10−8 in a.u.
In the following, we will consider only the case of a strongly informative prior for the variance. This means, we set d= 8 and denote the resulting PDF for the measurand by SIP (MC), indicating the use of a plain Monte Carlo sampling procedure.
3.2.3 Conventional Bayesian approach
We consider a fully Bayesian approach by rewriting the model for the measurand of the gauge block example (17) into a model for the observations LS and incorporating a prior for the measurand δL. The observation model function reads
and it is obvious that LS has a singularity when Z1 approaches 1. However, due to the actual structure of Z1, its realisations are well below 1 and no numerical issues are expected or have been observed. As prior for the measurand δL, a normal distribution with variance λ2 is assigned. This PDF is then combined with the  PDF for the parameter σ2 and the PDFs for Z1 and Z2 given by Type B information. In particular, we set
PDF for the parameter σ2 and the PDFs for Z1 and Z2 given by Type B information. In particular, we set
The variance of the measurand prior λ2 is chosen rather large with λ=103 nm to render the prior information vague.
For comparison with the informative Type A uncertainty evaluation, the degree of freedom parameter for the scale parameter is set to d = 8 to comply with the strongly informative prior. Computations for the Bayesian approach are carried out using MCMC and an analytic integration over σ2. The resulting marginal posterior PDF for the measurand is denoted by SIP (MCMC).
3.2.4 Results and discussion
In Figure 3 we compare the different state of knowledge PDFs for the measurand δL produced by the approaches discussed above. The solid blue line (NIP) corresponds to PDFs for the measurand that is derived using a noninformative prior for the location and scale parameter, whereas the solid red line (SIP (MC)) use an informative prior for the scale parameter σ. Both PDFs were computed using plain Monte Carlo sampling. The effect of the prior knowledge is clearly visible in Table 2, where the standard deviation is clearly reduced from NIP to SIP (MC) due to the incorporated prior knowledge. The dotted red line (SIP (MCMC)) shows the resulting posterior PDF from the conventional Bayesian approach, assuming a vague prior for the measurand and employing MCMC for the computation. It can be seen here that the SIP (MC) PDF and the SIP (MCMC) PDF are not identical. This is different to the example above but also clearly backed by Theorem 1, due to the nonlinearity of the model for the measurand (17). Therefore, it is not expected that prior ignorance about the location parameter μ is equivalent to prior ignorance about the measurand δL. We also show this effect quantitatively in Table 2.
This observation already shows a limitation of the plain Monte Carlo sampling based approach, as discussed in this work. Prior ignorance in one parameterisation does not equal prior ignorance in the other and vice versa. This is particularly true for highly non-linear models for the measurand. Therefore, metrologists need to be aware of this fact, not just for the setting of this work, but also when applying the JCGM 101 approach.
As for the Gaussian example above, the numeric values in Table 2 are subject to numerical variability. Therefore, three repeated computations have been performed using 108 samples for the NIP and the SIP (MC) approach, and 64 parallel chains with 106 samples each and a burn-in of 2000 samples for the MCMC computation. The mean values are stable for the given digits in Table 2. For the standard uncertainty, the NIP approach always yields the same result, the SIP (MC) yields [24.98, 24.98, 24.99] and SIP (MCMC) [23.35, 23.30, 23.36].
 |
Fig. 3 Results for the lognormal example of Section 3.2. We show the state of knowledge distributions for the measurand δL. The resulting PDF using the noninformative prior (NIP) is shown as a solid blue line and the informative prior (SIP (MC)) as a solid red line. The PDF resulting from the conventional Bayesian approach (SIP (MCMC)) using a vague measurand prior is shown by the dotted red line. |
4 Example for general parameter dependent data distributions
In this section we consider an example, that does not follow a location-scale distribution. However, the theory derived in Section 2 is still valid in the corresponding parametrisation of the data distributions. Moreover, the following cases can be tackled using pure Monte Carlo sampling. In the following, we will discuss an example from metrology where observations follow a Poisson distribution.
Consider the measurement of ionizing radiation with the aim to estimate the activity of some radiating specimen. The following model has been considered in the ISO 11929:2010 [31] and, using a (noninformative) reference prior with partial information for the activity, in [32].
The model for the activity is given by
Here, ρb denotes the background radiation rate that is subtracted from the overall gross radiation rate ρg. The difference is multiplied by some calibration factor v that models the detection efficiency of the measurement setup. For this calibration factor, a state of knowledge PDF πv can usually be elicited from expert knowledge. Here, a Gamma distribution is assigned to the calibration factor v, where the parameter of the distribution are chosen, such that, the estimate and standard uncertainty of v-1 basically coincide with the values given in [[32], p. S32, Table 1]. The background radiation rate and its uncertainty are usually obtained by calibration measurements. Also following the reference, the background radiation count rate ρb is assigned another Gamma distribution with estimate and standard uncertainty taken from the same table in the reference. Additionally, assume that Ng denotes the count number of the radiation measurement of the specimen and that this count can reasonably be accounted to a Poisson distribution Ng|ρg ∼ Po (ρgtg) with parameter ρg denoting the unknown Poisson rate and tg = 120 s denoting the known counting times of the measurement device. The observed count number Ng is given as Ng = 9.732s−1tg, cf. [32].
In this work and similar to the treatment in [32], we do not consider correlations between the background radiation rate and the overall gross radiation rate, since ρb is considered as a quantity with Type B information from historical measurements of the background and ρg is a quantity corresponding to current indications. If both ρb and ρg would be represented by indications, a multivariate consideration of an informative Type A evaluation would allow to include correlations.
4.1 JCGM 101 Type A uncertainty evaluation without prior knowledge
In the spirit of [1, clause 6.4.11.1], a flat prior is assigned to the Poisson rate parameter ρg. A subsequent Bayesian update yields a Gamma distribution with shape parameter Ng+1 and rate parameter tg to account for the counting times3. This PDF is subsequently used in conjunction with the PDFs of the other quantities ρb and v to perform a plain Monte Carlo propagation through the model for the activity (20) to obtain a corresponding PDF for A.
Since the assigned Gamma distribution for the quantity ρg with Type A information is the result of a Bayesian inference, the theoretical observations of Section 2 apply. Moreover, Theorem 1 can be used to conclude that the equivalent prior in the conventional Bayesian parametrization is given by
For the following computations, we make use both parameterisations to show numerically the validity of Theorem 1. To this end, on the one hand, we perform plain Monte Carlo sampling to estimate the PDF for the activity A using the JCGM 101 approach (JCGM 101 (MC)). On the other hand, we apply the Bayesian approach to the measurand directly using the joint prior (21) and MCMC for sampling. Since this approach is not considered in the JCGM 101, and we actually employ a flat prior for the activity A, we deviate from the notation and denote the resulting PDF as NIP (MCMC).
4.2 Informative Type A uncertainty evaluation
As in the previous examples, it is possible to obtain a PDF for ρg that is based on an informative Type A uncertainty evaluation using prior knowledge. The difference to the previous examples is that there is no distinction in location and scale parameter here. Nevertheless, prior knowledge about the unknown parameter ρg can be employed and still an efficient plain Monte Carlo sampling can be employed. For example, one might assume a priori that ρg is Gamma-distributed with fixed shape parameter ag and rate parameter βg obtained by some prior elicitation. Assigning this prior to ρg and performing a Bayesian update leads to a posterior PDF for the gross radiation rate
Combining this PDF independently with the available PDFs for the remaining quantities v and ρb, plain Monte Carlo sampling can again be used to generate samples from a PDF for the measurand, i.e., the activity A.
With the choice of a Gamma prior for the rate ρg, according to Theorem 1, the induced joint prior for the activity A, the background radiation rate ρb and the calibration factor v is given by
For the example, we elicited prior knowledge for ρg and about the parameter of the considered Gamma distribution, αg and βg, from the data given in [[33], Table 3 a)]. In particular, the mean of the prior PDF for ρg is set to 3.7 and the variance to 0.608. For the numerical computations, we employ plain Monte Carlo sampling using the informative Type A PDF (22) and the model for the measurand A and denote the resulting PDF for the measurand Inv χ2 (MC). Moreover, we perform MCMC sampling using a direct Bayesian approach and the prior (23). The resulting marginal posterior PDF for the activity A will be denoted Invχ2 (MCMC).
4.3 Conventional Bayesian approach
Following a direct Bayesian procedure for the equivalent observation model function ρg = νA + ρb with some joint prior π (A, ν, ρb) and Poisson distributed observations of ρg leads to the marginal posterior PDF for the activity A, that can be compared to the procedures given above. Using explicit prior knowledge about the activity allows to impose the natural assumption that the activity A is a non-negative quantity. To enforce this, we employ a left truncated Normal prior, starting from 0, centered at an estimate for A and scaled by a standard deviation λ. In this example, we use the estimate  according to [33, Table 3 a)] and as standard deviation λ=100. This choice renders the prior for the activity almost flat. Note that the computation of the posterior distribution using prior knowledge for the activity can, in general, only be treated using Markov Chain Monte Carlo or other sophisticated sampling techniques. In the following, the resulting PDF for the activity from this approach will be denoted by (Trun. Normal).
according to [33, Table 3 a)] and as standard deviation λ=100. This choice renders the prior for the activity almost flat. Note that the computation of the posterior distribution using prior knowledge for the activity can, in general, only be treated using Markov Chain Monte Carlo or other sophisticated sampling techniques. In the following, the resulting PDF for the activity from this approach will be denoted by (Trun. Normal).
4.4 Results and discussion
In Figure 4 we compare the resulting state of knowledge PDFs for the activity from the different models proposed. In blue, the JCGM 101 approach using Monte Carlo sampling (solid line) and the equivalent direct Bayesian approach using the prior (21) and MCMC (squares) are shown. Both PDFs are, up to numerical accuracy, identical, which can also be seen in quantitative terms in Table 3. In green, an informative inverse χ2 prior has been employed and used in conjunction with Monte Carlo sampling in terms of (22) (solid line) and MCMC sampling in terms of (23) (squares). Again, both PDFs are identical. Finally, as a dotted red line indicated by the employed truncated normal prior (Trun. Normal), a direct Bayesian approach for the measurand with a vague prior is shown. Also in this case, MCMC sampling has been used. While not perfectly aligned, the vague measurand prior results in a PDF for the activity that is close to the JCGM 101 approach. This is expected, since no significant prior knowledge has been incorporated by assuming A to be positive. The slight disagreement, in particular in terms of the mean, can be explained by the fact that the model for the measurand is again not linear in the Type A quantity ρg and, as shown in (21), another joint prior has to be employed to perfectly match the plain Monte Carlo sampling approach of JCGM 101. While the corresponding prior for the activity has to be flat, the term  requires a change of the Type B PDF for v, due to the nonlinearity of the model for the measurand. This effect has also been discussed in [16], where natural correlation between the measurand and the quantities of Type B has been identified to cause this discrepancy of the plain Monte Carlo and MCMC approaches. It is also to note that, the Monte Carlo approaches assume independence between the Type A quantity ρg and the Type B quantities (v,ρb). This means, using these approaches, the assumption that A ≥ 0 can only be enforced if the relevant domains of ρg and ρb are disjoint. Otherwise, informative prior knowledge for the measurand A or correlations between ρg and ρb may be required. This is, however, not the case in this example.
requires a change of the Type B PDF for v, due to the nonlinearity of the model for the measurand. This effect has also been discussed in [16], where natural correlation between the measurand and the quantities of Type B has been identified to cause this discrepancy of the plain Monte Carlo and MCMC approaches. It is also to note that, the Monte Carlo approaches assume independence between the Type A quantity ρg and the Type B quantities (v,ρb). This means, using these approaches, the assumption that A ≥ 0 can only be enforced if the relevant domains of ρg and ρb are disjoint. Otherwise, informative prior knowledge for the measurand A or correlations between ρg and ρb may be required. This is, however, not the case in this example.
For the graphs shown in Figure 4 and the numbers given in Table 3, the Monte Carlo results have been obtained using 108 samples and the MCMC results were obtained using 64 chains, each with 106 samples. Again, three independent repetitions of the experiments have been performed but no variation of the significant digits given for the numbers in Table 3 have been observed.
 |
Fig. 4 Results for the example of Section 4. We show the resulting state of knowledge distribution for the measurand A, denoting the activity of a radiating specimen in kBq. We show the PDFs resulting from the noninformative prior (JCGM 101) in blue, the informative χ2 prior in green and the truncated normal prior in red. (MC) denotes the use of plain Monte Carlo sampling and (MCMC) indicates Markov Chain Monte Carlo sampling. |
5 Conclusions
In this work we aimed to fill a theoretical gap that justifies the use of informative prior knowledge about the variance of a data distribution in conjunction with plain Monte Carlo sampling to achieve uncertainty estimation for a measurand in metrological applications. We have shown that such an approach is in line with a Bayesian inference by showing the equivalence of the resulting measurand PDF to a marginal posterior arising in a direct Bayesian uncertainty evaluation for the measurand. Notably, we were able to show this for data distributions beyond the usual normal case. Moreover, we explored possible limitations of such an approach, when comparing the results to that of a conventional Bayesian uncertainty evaluation. From a practical point of view, we provided examples beyond the case of normally distributed observations and we have shown how to incorporate prior knowledge about the variance of the data distribution.
The plain Monte Carlo sampling proposed allows for an efficient approach towards informative uncertainty evaluation in the presence of observations and metrologists are well familiar with these kind of computations, due to the well accepted guidance in JCGM 101. Our results allow them to use plain Monte Carlo sampling to also include prior knowledge about the precision of an employed measurement device. Since metrologists usually have well-founded prior knowledge about their employed devices, our results indicate a significant extension of the 101 machinery that can employ such prior knowledge and which is consistent with a Bayesian perspective.
Appendix A Proof of Theorem 1
Assume that X is set to the mean of the data distribution μ. While this assumption can be relaxed, it simplifies notation and presents a general case usually considered in metrology. This means, after observing the sample x1, … , xn, the PDF assigned to X is chosen as the marginal posterior πμ(m|x1, … , xn) from (1). Subsequent independent combination with πZ (z) and propagation through the model for the measurand yields the PDF πY. In particular, it holds
Using the prior πμ,σ and Bayes' formula for the marginal posterior for μ yields
Inserting this in (24) and using Fubini's theorem to exchange the integration order gives
Using the joint prior πY,Z,ρ given in Theorem 1 it follows
where the last proportionality corresponds to another application of Bayes' theorem from (4). This concludes the claim, since the last term on the right-hand-side is the marginal posterior for the measurand when using the prior πY,Z,σ.
An alternative formulation of these arguments and a proof for Corollary 2 is given below.
Using a change of variable with the relation X= g(Y, Z), the prior (5) induces the joint prior
on μ,Z,σ. Furthermore, the posterior distribution  is obtained by pushing
is obtained by pushing 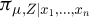 through the measurement model (2), leading to
through the measurement model (2), leading to
Integrating out σ yields  . Therefore,
. Therefore,  is obtained by propagating independently the Type B and the result of a Bayesian inference on the Type A.
is obtained by propagating independently the Type B and the result of a Bayesian inference on the Type A.
Appendix B Marginal Bayesian posterior for log-normal informative Type A evaluation
Consider independent recordings
with an informative prior, in terms of the data variance, given by π (μ, σ2) ∝ Iχ2 (ν0, τ2). Then, the marginal Bayes posterior for the location parameter μ is given by
Defining  and substitution of
and substitution of  and
and  yields.
yields.
Reformulating the result reveals the equivalence to a t-distribution PDF
We say, to comply with the usual parametrization convention of the t-distribution, the marginal Bayes posterior for the location parameter is a t-distribution with n+ v0 –1 degrees of freedom, shifted by the mean 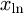 and scaled by
and scaled by 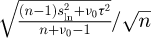 .
.
Appendix C Derivation and simulation for the lognormal distribution example
Consider the random variable Ls following a t-distribution with v > 2 degrees of freedom, shifted to the mean  and scaled by
and scaled by 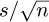 . The aim is now to construct another random variable Ls' that follows a lognormal distribution that has the same mean and variance as Ls.
. The aim is now to construct another random variable Ls' that follows a lognormal distribution that has the same mean and variance as Ls.
The mean and variance of Ls, following a scaled and shifted t-distribution is given by
Similiarly, a quantity Ls' that admits a lognormal distribution, as defined in (16), has mean and variance
Comparing both means and variances yields
For the considered example of Section 3.2 the parameter read v =18, 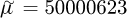 nm and s = 25 nm. Sampling from the resulting lognormal distribution yields the 10 simulated measurements in Table C1.
nm and s = 25 nm. Sampling from the resulting lognormal distribution yields the 10 simulated measurements in Table C1.
Simulated measurements of reference gauge block Ls in nm. We list 10 measurements that were generated from a lognormal distribution with parameters defined in Appendix C.
Funding
This article received no funding.
Conflicts of interest
The authors report no conflict of interest.
Data availability statement
This article has not generated or analyzed more data than already shown in the manuscript. Software can be made available upon request to the authors.
Author contribution statement
Conceptualization, M.M., S.D., S.P., N.F. and C.E.; Methodology, M.M, G.W., N.F. and C.E.; Software, M.M and S.P.; Validation, M.M, S.D., S.P., G.W., N.F. and C.E.; Formal Analysis, M.M, S.D., S.P., C.E.; Investigation, M.M, S.D., S.P., G.W., N.F. and C.E.; Resources, M.M.; Data Curation, M.M; Writing – Original Draft Preparation, M.M, S.D., S.P., N.F. and C.E.; Writing – Review & Editing, M.M, G.W. and C.E.; Visualization, M.M, S.D., S.P.; Supervision, N.F and C.E.
References
- Joint Committee for Guides in Metrology, Evaluation of measurement data — Supplement 1 to the Guide to the expression of uncertainty in measurement — Propagation of distributions using a Monte Carlo method. Sèvres, France: International Bureau of Weights and Measures (BIPM), 2008, BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, JCGM 101:2008. [Online]. Available: http://www.bipm.org/en/publications/guides/gum.html [Google Scholar]
- D.V. Lindley, The probability approach to the treatment of uncertainty in artificial intelligence and expert systems, Stat. Sci. 17–24 (1987) [Google Scholar]
- C.P. Robert, G. Casella, G. Casella, Monte Carlo statistical methods (Springer, 1999), vol. 2 [Google Scholar]
- K. Klauenberg, C. Elster, Markov chain Monte Carlo methods: an introductory example, Metrologia 53, S32 (2016) [CrossRef] [Google Scholar]
- E.T. Jaynes, Information theory and statistical mechanics, Phys. Rev. 106, 620 (1957) [CrossRef] [MathSciNet] [Google Scholar]
- R.E. Kass, L. Wasserman, The selection of prior distributions by formal rules, J. Am. Stat. Assoc. 91, 1343–1370 (1996) [CrossRef] [Google Scholar]
- K. Chaloner, Elicitation of prior distributions, Bayesian Biostat. 141, 156 (1996) [Google Scholar]
- A. O'Hagan, C.E. Buck, A. Daneshkhah, J.R. Eiser, P.H. Garthwaite, D.J. Jenkinson, J.E. Oakley, T. Rakow, Uncertain judgements: eliciting experts' probabilities (John Wiley & Sons, 2006) [CrossRef] [Google Scholar]
- G.A. Kyriazis, Comparison of GUM Supplement 1 and Bayesian analysis using a simple linear calibration model, Metrologia 45, L9 (2008) [CrossRef] [Google Scholar]
- C. Elster, B. Toman, Bayesian uncertainty analysis under prior ignorance of the measurand versus analysis using the Supplement 1 to the Guide: a comparison, Metrologia 46, 261 (2009) [CrossRef] [Google Scholar]
- I. Lira, D. Grientschnig, Equivalence of alternative Bayesian procedures for evaluating measurement uncertainty, Metrologia 47, 334 (2010) [CrossRef] [Google Scholar]
- A. Forbes, J. Sousa, The GUM, Bayesian inference and the observation and measurement equations, Measurement 44, 1422–1435 (2011) [CrossRef] [Google Scholar]
- J. Berger, The case for objective Bayesian analysis, Bayesian Anal. 1, 385–402 (2006) [Google Scholar]
- N. Giaquinto, L. Fabbiano, Examples of S1 coverage intervals with very good and very bad long-run success rate, Metrologia 53, S65 (2016) [CrossRef] [Google Scholar]
- G. Wübbeler, C. Elster, On the transferability of the GUM-S1 type A uncertainty, Metrologia 57, 015005 (2020) [CrossRef] [Google Scholar]
- M. Marschall, G. Wübbeler, C. Elster, Rejection sampling for Bayesian uncertainty evaluation using the Monte Carlo techniques of GUM-S1,Metrologia 59, 015004 (2021) [Google Scholar]
- A. O'Hagan, M. Cox, Simple informative prior distributions for Type A uncertainty evaluation in metrology, Metrologia 60, 025003 (2023) [CrossRef] [Google Scholar]
- J. Meija, O. Bodnar, A. Possolo, Ode to bayesian methods in metrology, Metrologia 60, 052001 (2023) [CrossRef] [Google Scholar]
- M. Evans, N. Hastings, B. Peacock, C. Forbes, Statistical distributions (John Wiley & Sons, 2011) [Google Scholar]
- V. Barnett, Probability plotting methods and order statistics, J. Royal Stat. Soc.: Ser. C (Applied Statistics) 24, 95–108 (1975) [Google Scholar]
- G. Wübbeler, M. Marschall, C. Elster, A simple method for Bayesian uncertainty evaluation in linear models, Metrologia 57, 065010 (2020) [CrossRef] [Google Scholar]
- EA Laboratory Committee and others, Expression of the Uncertainty of Measurement in Calibration, ” European Co-Operation for Accreditation, Paris, France, ReportNo. EA-4/02 M: 2013 (2013). Available: http://www.european-accreditation.org/publication/ea-4-02-m-rev01-september-2013 [Google Scholar]
- S. Demeyer, N. Fischer, C. Elster, Guidance on Bayesian uncertainty evaluation for a class of GUM measurement models, Metrologia 58, 014001 (2020) [Google Scholar]
- A. Gelman, J. Carlin, H. Stern, D. Rubin, Bayesian Data Analysis (Chapman andS Hall-CRC, 2003) [CrossRef] [Google Scholar]
- A. O'Hagan, J. Forster, Kendall's Advanced Theory of Statistics, volume 2B, Bayesian Inference (Arnold, 2004) [Google Scholar]
- A. van der Veen, Bayesian inference in r and rstan, in Good Practice in Evaluating Measurement Uncertainty − Compendium of examples (2021), pp. 21–28. Available: http://empir.npl.co.uk/emue/wp-content/uploads/sites/49/2021/07/Compendium_ M36.pdf [Google Scholar]
- I. Lira, Analysis and comparison of Bayesian methods for type A uncertainty evaluation with prior knowledge, Ukrainian Metrolog. J. 4, 3–6 (2022) [CrossRef] [Google Scholar]
- D. Foreman-Mackey, D.W. Hogg, D. Lang, J. Goodman, “emcee: the MCMC hammer,” Publications of the Astronomical Society of the Pacific 125, no. 925 (2013) p. 306 [CrossRef] [Google Scholar]
- C.F. Carobbi, M. Cati, L.M. Millanta, Using the log-normal distribution in the statistical treatment of experimental data affected by large dispersion, in 2003 IEEE Symposium on Electromagnetic Compatibility. Symposium Record (Cat. No. 03CH37446) 2. IEEE (2003) pp. 812–816 [CrossRef] [Google Scholar]
- W.R. Ott, A physical explanation of the lognormality of pollutant concentrations, J. Air Waste Manag. Assoc. 40, 1378–1383 (1990) [CrossRef] [PubMed] [Google Scholar]
- ISO, 11929: Determination of the Characteristic Limits (Decision Threshold, Detection Limit and Limits of the Confidence Interval) for Measurements of Ionizing Radiation: Fundamentals and Application (International Organization for Standardization, 2010) [Google Scholar]
- O. Bodnar, R. Behrens, C. Elster, Bayesian inference for measurements of ionizing radiation under partial information, Metrologia 54, S29 (2017) [CrossRef] [Google Scholar]
- O. Bodnar, G. Wübbeler, C. Elster, On the application of Supplement 1 to the GUM to non-linear problems, Metrologia 48, 333 (2011) [CrossRef] [Google Scholar]
Cite this article as: Manuel Marschall, Séverine Demeyer, Sébastien Petit, Gerd Wübbeler, Nicolas Fischer, Clemens Elster, Utilizing prior knowledge about the measurement process for uncertainty evaluation through plain Monte Carlo sampling, Int. J. Metrol. Qual. Eng. 15, 14 (2024)
All Tables
Statistical assessment of the resulting PDFs with values given in mg. From left to right we collect the mean estimate, the standard uncertainty given by the standard deviation of the PDF, and a 95% coverage interval. Also, the total number of samples generated and the corresponding computation is time is shown. The standard deviation of the measurand for the NIP approach is not defined, since only three measurements are present.
Simulated measurements of reference gauge block Ls in nm. We list 10 measurements that were generated from a lognormal distribution with parameters defined in Appendix C.
All Figures
 |
Fig. 1 Graphical abstract for the methodology and contributions in this work. Informative Bayesian Type A uncertainty evaluation and subsequent Monte Carlo propagation to obtain a state of knowledge distribution for the measurand is presented. If independent sampling from the marginal posterior πμ(m|x1, … , xm), cf. (1), is possible, plain Monte Carlo sampling can be used to sample from the posterior distribution for the measurand by combining samples from πμ(m|x1, … , xn) with samples from the Type B state of knowledge PDF πZ (z). The theoretical justification is given in Section 2 and practical examples are given in Section 3. |
| In the text | |
 |
Fig. 2 Results for the example of Section 3.1. We show the resulting state of knowledge distribution for the measurand mX, denoting the deviation of a weight of mass 10 kg. We show the PDFs resulting using the noninformative prior (NIP) in blue, the mildly informative prior (MIP) in green and the strongly informative prior (SIP) in red. Both, MIP and SIP, are computed once using plain Monte Carlo (MC) and once using a vague prior for the measurand and MCMC. |
| In the text | |
 |
Fig. 3 Results for the lognormal example of Section 3.2. We show the state of knowledge distributions for the measurand δL. The resulting PDF using the noninformative prior (NIP) is shown as a solid blue line and the informative prior (SIP (MC)) as a solid red line. The PDF resulting from the conventional Bayesian approach (SIP (MCMC)) using a vague measurand prior is shown by the dotted red line. |
| In the text | |
 |
Fig. 4 Results for the example of Section 4. We show the resulting state of knowledge distribution for the measurand A, denoting the activity of a radiating specimen in kBq. We show the PDFs resulting from the noninformative prior (JCGM 101) in blue, the informative χ2 prior in green and the truncated normal prior in red. (MC) denotes the use of plain Monte Carlo sampling and (MCMC) indicates Markov Chain Monte Carlo sampling. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.