| Issue |
Int. J. Metrol. Qual. Eng.
Volume 9, 2018
|
|
|---|---|---|
| Article Number | 12 | |
| Number of page(s) | 5 | |
| DOI | https://doi.org/10.1051/ijmqe/2018012 | |
| Published online | 16 November 2018 | |
Research Article
Evaluation of measurement uncertainty for the determination of the mechanical resistance of the brick samples by using uniaxial compressive strength test
1
Department of Production Management, Faculty of Mechanical Engineering, Polytechnic University of Tirana,
Mother Teresa No. 3, 1001
Tirana, Albania
2
Department of Mathematical Engineering, Faculty of Mathematical & Physical Engineering, Polytechnic University of Tirana,
Mother Teresa No. 3, 1001
Tirana, Albania
3
Department of Metallurgy Engineering, Faculty of Mechanical Engineering, University of Sultan Ageng Tirtayasa,
Jl. Jend Sudirman Km. 3,
Cilegon, Banten
42435, Indonesia
* Corresponding author: kdhoska@upt.al
Received:
8
December
2017
Accepted:
3
October
2018
Clay bricks are the most important engineering materials that can influence the quality of the construction. The quality control of the clay bricks is of prime importance to improve the quality of engineering construction. The qualities of bricks for construction applications should be checked for various types of inspection services. In this article, our inspection service was focused on compression strength test on bricks to determine their mechanical resistance and suitability for construction work. The accurate method for clay brick's production measurements has been elaborated using uniaxial compressive strength testing machine. The method was tested for a rectangular clay brick manufactured with size approximately 250 mm × 250 mm × 200 mm. The measurement method and standard uncertainty estimation of uniaxial compressive strength are briefly described in this article.
Key words: clay brick&apos / s production / inspection services / uniaxial compressive strength / standard uncertainty
© K. Dhoska et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Clay brick materials are the oldest building materials in the world and are still immensely popular [1]. It can be used for a variety of applications such as single-family houses or apartment blocks, office or public buildings, and for all architectural styles.
In the last two decades, many manufacturing companies in Albania have been focused on the production and distribution of brick materials made of clay. Furthermore, Edilcentro Ltd. is one of the leading companies in Albania in the field of bricks' production of high quality. In this company, the phases of clay bricks' production are under automatic control and permanent supervision of the technological process [2]. Figure 1 depicts the technological scheme of clay brick's production.
According to this scheme of the automation process, it is clear that inspection services play an important role in ensuring the quality of the clay brick's production. The qualities of bricks for construction applications should be checked for various types of inspection services. Some of the inspection services would be related to absorption test, compression strength test, hardness test, shape and size, color test, soundness test, structure of brick, and presence of soluble salts.
Our research work has been focused on compression strength test on bricks to determine their mechanical resistance and suitability for the construction work. One of the basic and most used methods of testing which is performed on brick samples is the determination of uniaxial compressive strength [3]. Similar testing has been performed successfully on other types of materials such as concrete, rocks, and metals with some differences in testing procedures and minimum measurement equipment properties [4–7]. Furthermore, according to the American Society for Testing and Materials (ASTM) specifications, we have performed compression testing for the determination of the properties of clay brick materials.
In this article, we have briefly described the measurement method and standard uncertainty estimation of measured uniaxial compressive strength which would depend on the force applied to the sample.
 |
Fig. 1 Technological scheme of clay brick's production. |
2 Measurement method
The uniaxial compressive strength machine is located in the laboratory of the manufacturing company Edilcentro Ltd., Albania. The complete range of the uniaxial compression strength machine was designed to meet the demands of our laboratory as shown in Figure 2. Compressive load was applied in displacement control on clay bricks using MTS servo-hydraulic actuator. Load and displacement measurements were recorded in real time using a computer-based data acquisition system.
The measuring range of the uniaxial compression testing machine varied from 0 to 500 kN. The function of the uniaxial compression testing machine consists in applying the load to the surface area of materials that will be tested. The load frame provides the stability required for accurate test results. A small number of indirect compressive strength tests have been developed, primarily in order to allow in situ quality control testing of materials. The compression testing was performed according to ASTM and ISO specifications [5–8]. In the present test set-up, 10 specimens of clay bricks were tested for determining their mechanical resistance. The manufactured clay bricks had approximate length, width, and height of 250, 250, and 200 mm, respectively.
In the measurements, the clay bricks were generally placed in-between two plates that distribute the applied load across the entire surface area of two opposite faces of the test sample and then the plates are pushed together by a uniaxial compressive testing machine. A compressed clay brick was usually shortened in the direction of the applied forces, and load measurements were recorded in real time using a computer-based data acquisition system. The uniaxial compressive strength of the test specimens was calculated by dividing the maximum compressive load on the specimen by the initial cross-sectional area. A compressive strength measurement and the surface area of each clay brick are given in Table 1.
 |
Fig. 2 Test set-up for compression testing of clay brick. |
Summary of test results on clay bricks.
3 Uncertainty of uniaxial compressive strength
Uniaxial compressive strength is the quantity that is indirectly determined by the measurement which depends on the force applied to the sample. Sample stress σ of uniaxial compressive strength is evaluated as the ratio of maximum applied force Fmax and sample cross-sectional area A in the beginning of the test according to equation (1).
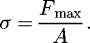 (1)
(1)
In accordance with equation (1), the measurement uncertainty of stress will depend uncertainty of the force and the uncertainty of cross-sectional area. A Guide to the Expression of Uncertainty in Measurement (GUM) has been used to establish the general rules for identifying sources of uncertainty and evaluating the measurement uncertainty [9]. Before starting an evaluation of uncertainty, the uniaxial compressive strength measurement model has been defined by taking into account influence sources of uncertainty which can be expressed as follows [9–12]:
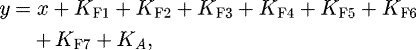 (2)
where x is the measurement value of the uniaxial compressive strength, KF1 is the correction from calibration of uniaxial compressive strength machine, KF2 is the correction that arises from load application rate to sample test, KF3 is the correction that arises from the preservation condition effect on compression resistance of a sample, KF4 is the correction that arises from the effect of planarity on compression resistance of a sample, KF5 is the correction with respect to the angle of the surface plane between the sides, KF6 is the correction that comes from sample centering, KF7 is the correction from reading of applied load, and KA is the correction that arises from reading of the sample cross-sectional area.
(2)
where x is the measurement value of the uniaxial compressive strength, KF1 is the correction from calibration of uniaxial compressive strength machine, KF2 is the correction that arises from load application rate to sample test, KF3 is the correction that arises from the preservation condition effect on compression resistance of a sample, KF4 is the correction that arises from the effect of planarity on compression resistance of a sample, KF5 is the correction with respect to the angle of the surface plane between the sides, KF6 is the correction that comes from sample centering, KF7 is the correction from reading of applied load, and KA is the correction that arises from reading of the sample cross-sectional area.
Based on the law of propagation of uncertainty and uncertainty of input quantities, we can evaluate combined uncertainty as expressed below:
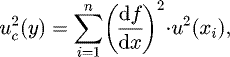 (3)
where u(xi) is the standard uncertainty of the input quantities and ci = df/dx is the sensitivity coefficient. According to the input quantities, the combined uncertainty could be expressed as follows:
(3)
where u(xi) is the standard uncertainty of the input quantities and ci = df/dx is the sensitivity coefficient. According to the input quantities, the combined uncertainty could be expressed as follows:
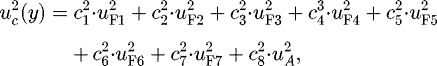 (4)where uF1 is the calibration uncertainty of uniaxial compressive strength machine, uF2 is the uncertainty of the load application rate to sample test, uF3 is the uncertainty of the preservation condition effect on compression resistance of a sample, uF4 is the uncertainty of the effect of planarity on compression resistance of a sample, uF5 is the uncertainty with respect to the angle of the surface plane between the sides, uF6 is the uncertainty of sample centering, uF7 is the standard uncertainty of the reading of applied load, and uF8 is the standard uncertainty of the reading of sample cross-sectional area.
(4)where uF1 is the calibration uncertainty of uniaxial compressive strength machine, uF2 is the uncertainty of the load application rate to sample test, uF3 is the uncertainty of the preservation condition effect on compression resistance of a sample, uF4 is the uncertainty of the effect of planarity on compression resistance of a sample, uF5 is the uncertainty with respect to the angle of the surface plane between the sides, uF6 is the uncertainty of sample centering, uF7 is the standard uncertainty of the reading of applied load, and uF8 is the standard uncertainty of the reading of sample cross-sectional area.
As the calibration uncertainty contribution, the specifications of the uniaxial compressive strength machine are used [8,9,13]:
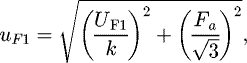 (5)
where UF1 is the expanded calibration uncertainty of the machine which corresponds to 250 N with a coverage factor k = 2 and Fa is the test device scale which corresponds to 1000 N.
(5)
where UF1 is the expanded calibration uncertainty of the machine which corresponds to 250 N with a coverage factor k = 2 and Fa is the test device scale which corresponds to 1000 N.
Since it was difficult to quantify more accurately the effect of load application rate on the sample test, we have assumed for simplification of the technical documents that evaluation of the uncertainty will be expressed as follows [6,11–14]:
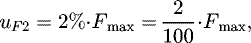 (6)
where Fmax is the maximum applied force on the clay brick materials. We have used similar assumptions for the evaluation of the other sources of uncertainty which can be expressed as follows:
(6)
where Fmax is the maximum applied force on the clay brick materials. We have used similar assumptions for the evaluation of the other sources of uncertainty which can be expressed as follows:
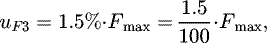 (7)
(7)
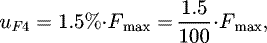 (8)
(8)
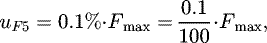 (9)
(9)
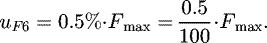 (10)
(10)
The standard uncertainty due to the reading of indications of applied load is calculated as the standard deviation of the readings of applied loads SF7, expressed as follows [8,9]:
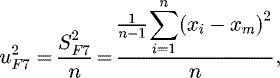 (11)
where n is a complete set of measurement values, xi is the individual measurement value, and xm is the arithmetic mean of individual measurements.
(11)
where n is a complete set of measurement values, xi is the individual measurement value, and xm is the arithmetic mean of individual measurements.
The standard uncertainty due to the reading of indications of the sample cross-sectional area uA is expressed as follows [15]:
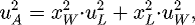 (12)
where xW and xL are the reading values of the width and length for the sample cross-sectional area which can be evaluated as follows:
(12)
where xW and xL are the reading values of the width and length for the sample cross-sectional area which can be evaluated as follows:
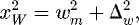 (13)
(13)
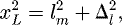 (14)where lm is the mean value of length, wm is the mean value of the width, Δl is the correction from readings of length, and Δw is the correction from readings of width which are Δl = Δw= 0.
(14)where lm is the mean value of length, wm is the mean value of the width, Δl is the correction from readings of length, and Δw is the correction from readings of width which are Δl = Δw= 0.
The standard uncertainties of the length uL and width uW are evaluated as follows:
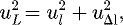 (15)
(15)
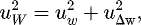 (16)
where ul and uw are the standard deviations of the readings of length and width, respectively, and uΔl and uΔw are the relative uncertainties of length and width, respectively, which are uΔl = uΔw = 0.05 mm.
(16)
where ul and uw are the standard deviations of the readings of length and width, respectively, and uΔl and uΔw are the relative uncertainties of length and width, respectively, which are uΔl = uΔw = 0.05 mm.
The final evaluation of equation (12) can be expressed by equation (17):
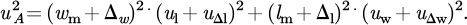 (17)
(17)
The sensitivity coefficient of the applied force and cross-sectional area were calculated from equation (1).
In the end, we can evaluate combined standard uncertainties according to equation (6), and expanded uncertainty U is obtained through multiplication by coverage factor k = 2, as expressed in the following equation:
 (18)
(18)
Furthermore, using the above equations, we can summarize in Table 2 all the sources of uncertainties associated with their values.
According to equations (1) and (18), the estimated results of the sample stress of uniaxial compressive strength have shown that expanded uncertainty of 2.23 N/mm2 (estimated value) was 0.28 N/mm2.
As can be seen, the larger uncertainty components arise from load application rate to sample test, preservation condition effect on compression resistance of a sample, effect of planarity on compression resistance of a sample, and sample centering.
The difficulties in quantifying more accurately the effect of a load application rate to sample test, preservation condition effect on compression resistance of a sample, and effect of planarity on compression resistance of a sample have influenced the uncertainty measurement results. The alignment in manual way of the sample centering has also influenced the uncertainty measurement results. Therefore, further research work will be focused on the improvement of the largest uncertainty components.
Sources of uncertainties associated with their values.
4 Conclusions
This article describes measurement method and contributions to uncertainty of results obtained by testing of clay brick's production. The accuracy of clay brick's production results can be extracted through evaluation of measurement uncertainty. Our measurement model can be used for most of the rectangular types of clay brick's production measured by uniaxial compressive testing machine at good accuracy. The method was tested for a rectangular clay brick manufactured with size approximately 250 mm × 250 mm × 200 mm. The expanded uncertainty of 2.23 N/mm2 was 0.28 N/mm2. The thorough uncertainty analysis has shown that larger uncertainty arises from load application rate to sample test, preservation condition effect on compression resistance of a sample, effect of planarity on compression resistance of a sample, and sample centering.
Acknowledgments
The authors gratefully acknowledge the Edilcentro Ltd. for providing the clay bricks used in this work and Polytechnic University of Tirana for partial funding of this work.
References
- Wienerberger Clay Building. Available at https://clay-wienerberger.com/expertise/clay-building-materials-advantages (accessed 1 December 2017). [Google Scholar]
- Edilcentro Ltd. Available at http://www.gruppoedilcentro.com/en/pages/prezantimi/index.htm (accessed 12 November 2017). [Google Scholar]
- D. Kuhinek, I. Zorić, P. Hrženjak, Measurement uncertainty in testing of uniaxial compressive strength and deformability of rock samples, Meas. Sci. Rev. 11, 4 (2011) [Google Scholar]
- ASTM.D. 2938-95:2002, Standard Test Method for Unconfined Compressive Strength of Intact Rock Core Specimens (ASTM, West Conshohocken, PA, 2002). [Google Scholar]
- B.H. Kaushik, C.R. Durgesh, K.J. Sudhir, Uniaxial compressive stress-strain model for clay brick masonry, Curr. Sci. 92, 4 (2007) [Google Scholar]
- EN 1239 0-3:2009, Testing Hardened Concrete − Part 3: Compressive Strength of Test Specimens (Brussels, Belgium, 2009). [Google Scholar]
- ISO 6892-1:2009, Metallic Materials − Tensile Testing: I. Method of Test at Room Temperature (Geneva, Switzerland, 2009). [Google Scholar]
- ASTM C67: 17, Standard Test Methods for Sampling and Testing Brick and Structural Clay Tile (West Conshohocken, PA, 2017). [Google Scholar]
- ISO/IEC Guide 98:1995, Guide to the Expression of Uncertainty in Measurement (ISO, Geneva, Switzerland, 1995). [Google Scholar]
- ASTM C 1314-00a:2001, Standard Test Method for Compressive Strength of Masonry Prisms, in Masonry Test Methods and Specifications for the Building Industry (American Society for Testing and Materials, Pennsylvania, 2001). [Google Scholar]
- JCGM 100:2008, Evaluation of Measurement Data − Guide to the Expression of Uncertainty in Measurement. [Google Scholar]
- JCGM 102:2011, Evaluation of Measurement Data − Supplement 2 to the “Guide to the Expression of Uncertainty in Measurement” − Extension to Any Number of Output Quantities. [Google Scholar]
- ASEW-092 Compression Testing Machine Brochure. Available at http://www.asewindia.com/concrete-testing-equipments.html [Google Scholar]
- EN 196-1:2016, Methods of Testing Cement. Determination of Strength (European Standard Normative). [Google Scholar]
- EA-4/02 M: 2013, Evaluation of the Uncertainty of Measurement in Calibration (European Accreditation Laboratory Committee). [Google Scholar]
Cite this article as: Klodian Dhoska, Saimir Tola, Agus Pramono, Indrit Vozga, Evaluation of measurement uncertainty for the determination of the mechanical resistance of the brick samples by using uniaxial compressive strength test, Int. J. Metrol. Qual. Eng. 9, 12 (2018)
All Tables
All Figures
 |
Fig. 1 Technological scheme of clay brick's production. |
| In the text | |
 |
Fig. 2 Test set-up for compression testing of clay brick. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


