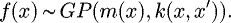| Issue |
Int. J. Metrol. Qual. Eng.
Volume 12, 2021
Topical Issue - Advances in Metrology and Quality Engineering
|
|
|---|---|---|
| Article Number | 22 | |
| Number of page(s) | 6 | |
| DOI | https://doi.org/10.1051/ijmqe/2021020 | |
| Published online | 10 September 2021 | |
Research article
Pointing error compensation of electro-optical detection systems using Gaussian process regression
1
Key Laboratory of Optoelectronic Devices and Systems of Ministry of Education and Guangdong Province, College of Physics and Optoelectronic Engineering, Shenzhen University, Shenzhen Guangdong 518060, PR China
2
MOEMS Education Ministry Key Laboratory, Tianjin University, Tianjin 300072, PR China
3
College of Engineering, Design and Physical Sciences, Brunel University London, Uxbridge UB8 3PH, UK
4
National Physical Laboratory, Hampton Road, Teddington, Middlesex TW11 0LW, UK
* Corresponding author: QingPing.Yang@brunel.ac.uk
Received:
26
February
2021
Accepted:
10
August
2021
Pointing accuracy is an important indicator for electro-optical detection systems, as it significantly affects the system performance. However, as a result of misalignment, nonperpendicularity in the manufacturing and assembly processes, as well as the sensor errors such as camera distortion and angular sensor error, the pointing accuracy is significantly affected. These errors should be compensated before using the system. Parametric models are firstly proposed to compensate for the errors, whilst the semi-parametric models with the nonlinearity added are also put forward. Both methods should analyse the parametric part first, which is a complicated and inaccurate process. This paper presents a nonparametric model, without any prior information about mechanical dimensions, etc. It depends only on the test data. Gaussian Process regression is used to represent the relationship between data and predict the compensated output. The test results have shown that the regression variances have decreased by more than an order of magnitude, and the means have also been significantly reduced, with the pointing error well improved. The nonparametric model based on Gaussian Process is thus demonstrated to be an effective and powerful tool for the pointing error compensation.
Key words: Gaussian process regression / pointing error / nonparametric model / EODS
© Q. Tang et al., Published by EDP Sciences, 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Electro-optical detection systems (EODSs) have been widely used to collect targets location information with visible and infrared cameras in many applications, such as vehicles, ships, aircrafts, and spacecraft. It always contains a biaxial mechanical structure, the camera is fixed on the inner frame. With the two axial motor rotation, the camera can search and track the target in a certain angle range. As the pointing accuracy significantly affects the target tracking and location, it is necessary to obtain the pointing direction of line of sight (LOS) accurately [1,2]. The pointing error can be approximately divided into two categories, the first is the mechanical error, which is caused by misalignment, nonperpendicularity, etc. in the manufacturing and assembly processes. The second is the sensor errors, including camera error and angular sensor error. A minor bias of LOS will result in significant deviation over a long location distance. It is thus imperative to model and compensate for these errors to improve the pointing accuracy [3,4]. Parametric compensation model is firstly proposed to compensate for the errors. In reference [3], each geometric error source was analysed, error synthesis was the final pointing error. Reference [5] proposed a parametric compensation model based on the integrant errors, which presented the distributions of each error source for radio telescopes in detail. Since the platform of EODS is similar to that of radio telescope, the analysis method is also applicable to the EODS. Reference [6] analysed the mechanical errors of an integrated time delay integration charge coupled device aerial camera and established a pointing error model based on the ray tracing algorithm, and a genetic algorithm was performed to identify the model parameters. Since the platform of EODS is similar to that of radio telescope, the analysis method is also applicable to the EODS. In reference [7], a pointing error model caused by the machining errors and installation errors of ground based telescope is established, and a simulated annealing algorithm is used to correct the parameters of pointing error model to improve the detection accuracy. Reference [8] considered the detection and the launch system with different wavelength, the error between the detection and the launch was analysed and the relationship was calculated. Meanwhile, the semiparametric model has also been widely used for pointing accuracy improvement, which is built on the parametric model. Semiparametric models add extra nonlinear error factors, model accuracy is more accurate. Reference [9] firstly obtained the integrant error model and then applied semiparametric compensation model to improve the pointing accuracy of the EODS. In reference [10], a telescope's kinematics model was established based on the Denavit-Hartenberg convention, mechanical errors were analysed, and a semi-parametric model was established for pointing error compensation. Reference [11] firstly established a basic parametric model of point error with clear physical significance by analysing the physical structure and error source, and a semi-parametric regression model was proposed to improve the system accuracy. Reference [12] proposed a new model named Allan variance based semi-parametric model to improve the point precision for alt-az telescopes. Similar semi-parametric models were also presented in [4,13], which demonstrated semiparametric model's better performance. Both for parametric and semi-parametric models, the parametric part should be analysed first, including mechanical dimensions, installation mode and tolerance control, it is a very complicated process to establish each integrant error propagation model. Different from above two types of models, nonparametric model is established without any prior information about mechanical dimensions, etc. It depends only on the test data. As a result, the modelling process becomes simpler. Hence, we propose a nonparametric model based on Gaussian Process (GP) regression to analyse and improve the pointing accuracy.
2 Gaussian process regression
GP regression is a kind of machine learning problems, which are broadly divided into three fundamental classes: supervised learning, unsupervised learning and reinforcement learning. Supervised learning is the learning of input-output mappings from the training data. As generally used covariance functions, GP is a simple and general class of probability distributions on functions [14]. Since proposed by O'Hagan in 1978 [15], GP regression model has been widely used to perform Bayesian nonlinear regression and classification problems in machine learning due to its good performance in practice and desirable analytical properties [16–19].
2.1 Gaussian process
From the view of function space, the definition of GP in [10] shows a GP is collection of random variables, any finite number of which have a joint Gaussian distribution. It can be completely represented by its mean function and covariance function. The mean function m (x) and covariance function k (x, x′) of a mapping function f (x) are defined as [17]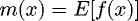 (1)
(1)
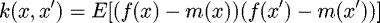 (2)
(2)
Given a data set X consisting of n input vectors, X = [x1, x2 ⋯ xn] (x εRD), and the corresponding output vectors, Y = [y1, y2 ⋯ yn]. We assume that Y is noisily observed from the underlying functional mapping f (X). (4)where σ2 is the variance of the noise, I is the identity matrix. Equivalently, the noise model can also be denoted as [17]
(4)where σ2 is the variance of the noise, I is the identity matrix. Equivalently, the noise model can also be denoted as [17]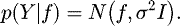 (5)
(5)
The main regression task is to estimate the mapping function f (X) from the training data X and Y. The primary objective is to give the optimal estimate Y* from the test input vectors, X* = [x*1, x*2 ⋯ x*m].
A GP defines a probability distribution on functions p (f), which can be used as a Bayesian prior for the regression estimate, and Bayesian inference is used to make predictions from data as shown in (6) [17]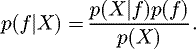 (6)
(6)
We normally assume the zero mean GP prior on f satisfies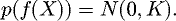 (7)
(7)
where K is the covariance of X. The marginal likelihood can be obtained by integrating over the unobserved function f [17],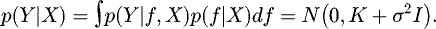 (8)
(8)
As the mean is assumed zero, the significant factor affecting the regression estimate result is the covariance function. A commonly used form is the ‘squared exponential’, shown in (9) [17]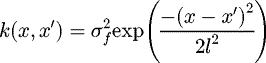 (9)where
(9)where 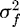 is the maximum allowance variance, l is the length factor. Then the covariance K can be computed as
is the maximum allowance variance, l is the length factor. Then the covariance K can be computed as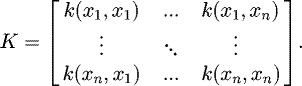 (10)
(10)
2.2 Prediction
Considering the test input, X*, we have the covariance matrices of X* to X* and X* to X.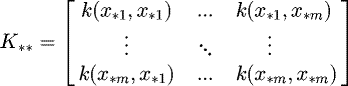 (11)
(11)
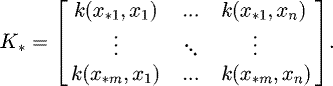 (12)
(12)
As the premise, we assumed the data complying with a multivariate Gaussian distribution, the multivariate distribution with additive independent identically distributed noise is presented as [17]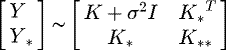 (13)where
(13)where 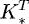 is the transposition of K*. Then the conditional distribution of Y* given Y is [17]
is the transposition of K*. Then the conditional distribution of Y* given Y is [17]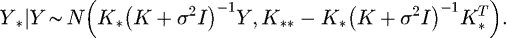 (14)
(14)
The optimal estimate for the output is the mean in (14)
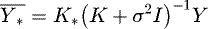 (15)
(15)
and its uncertainty is the variance in (14)
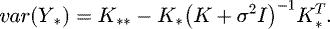 (16)
(16)
2.3 Parameter selection
Take the squared exponential covariance function as an example, in order to ensure GP regression to be a practical tool in pointing error compensation, we have to select proper σf and l for (9) to obtain the best regression. We define the hyper-parameters of the covariance function as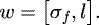 (17)
(17)
According to Bayes' theorem in (6), to obtain the maximum posteriori estimate of w, p(w|X, Y), we should maximize the p(Y|X, w), as obtained in (8). To simplify the computation, the log marginal likelihood is often used [17] (18)
(18)
Through multivariate optimization algorithm, such as conjugate gradients, Nelder-Mead simplex, etc., we could determine the proper hyper parameters [18].
3 Model selection
During the covariance computation, there are plenty of possible covariance functions to choose from, including squared exponential, polynomial, neural network, etc., each has a number of undetermined hyper-parameters. Choosing proper covariance functions for a particular application is vital to the regression. A complex covariance function with many undetermined parameters needs a huge amount of test data, and it is difficult to converge to the optimal solution. According to the experimental data and the complexity of EODS, we chose to employ the squared exponential covariance function, which is universal and easily convergent. The general form [17] is shown as: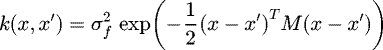 (19)
(19)
where the matrix M may be one of the following forms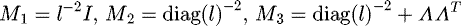 (20)where l is a vector of positive values l = l1, l2 ⋯ lD; Λ is a D × k(k < D) matrix.
(20)where l is a vector of positive values l = l1, l2 ⋯ lD; Λ is a D × k(k < D) matrix.
In this paper, as the inputs are two dimensional, we applied the first form in (20) to estimate the overall trend of the pointing error, and utilized the second to remedy the differences of each dimension. The final covariance function is shown in (21)
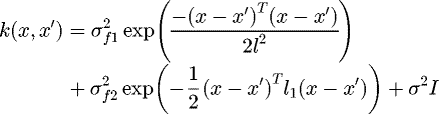 (21)where l1 = diag (l11, l12).
(21)where l1 = diag (l11, l12).
Here, it should be noted that “nonparametric” is raised corresponding to “parametric” and “semiparametric”. “Parametric” model contains determined error sources and their propagation models, and the compensation is targeted. “Semiparametric” model includes both “parametric” part mentioned above, and “nonparametric” part denoting the nonlinear error sources, which cannot be expressed by specific formulas. “Nonparametric” in this paper means there are no determined error sources in the compensation model, and the error is compensated as a whole.
4 Test results
The data acquisition system contains a high precision turntable, an autocollimator and the EODS, as shown in Figure 1. The test angular range is −20°∼20° for azimuth, and −20°∼10° for elevation. The turntable generates precision rotatory angles, the EODS rotates in the opposite direction, and the autocollimator gives the pointing error readout.
After the systemic error of the test system due to misalignment is compensated for, we apply GP regression to estimate the pointing errors using Gaussian processes for machine learning toolbox [19]. The azimuth and elevation results are shown in Figures 2–4 and Tables 1 and 2.
Figure 2 presents the regression results for azimuth and elevation over the measuring domain, which shows apparent differences in the components of pointing error, azimuth error is more significant. Figure 3 gives a detailed description of the prediction results in azimuth and elevation for the training data. Combined with Table 1, both the mean and variance values are greatly reduced after compensation. Figure 4 shows the comparisons of the actual measuring results and GP prediction results. The variances in the azimuth and elevation axes have decreased from 0.0258 (°)2 and 0.0017 (°)2 to 0.0014 (°)2 and 0.0010 (°)2, respectively, improved by more than an order of magnitude, and the means are also significantly reduced. These all illustrate that the proposed nonparametric compensation model based on GP regression is effective and successful.
Among the three types of compensation models [4], both nonparametric and semiparametric models present a better performance than parametric model based on integrant errors. Although the semiparametric model should be theoretically more advantageous as a result of its applicability in linear and nonlinear problems, in this paper the nonparametric model based on GP regression achieved the same effect as the semiparametric model. On the other hand, without complicated modelling process for each integrant error source, the nonparametric is more convenient than the other two models. Hence, the nonparametric method is effective and recommendable.
 |
Fig. 1 Test apparatus of the EODS. |
Compensation results comparison.
Prediction results comparison among different models for test data.
 |
Fig. 2 Pointing error regression for azimuth and elevation. |
 |
Fig. 3 Prediction results for the training data. |
 |
Fig. 4 Prediction results for the test data. |
5 Conclusions
Pointing accuracy of EODS significantly affects the target tracking and location, it is necessary to obtain the pointing direction of LOS accurately. As for misalignment, nonperpendicularity, etc. in the manufacturing and assembly processes, this paper established a nonparametric compensation model based on GP regression. Different from the parametric and semi-parametric models, which should analyse the parametric part based on the physical structure and error source, it is complicated and inaccurate. This paper only focused on the test data, and it realised pointing error compensation based on the Gaussian process regression. It firstly obtained the marginal likelihood of the training data, and then the prediction equations by means of choosing proper covariance functions. To obtain the optimal hyper parameters, the maximisation of the log marginal likelihood equation was performed. The hyper parameters were finally utilized in pointing error regression of the EODS. The test results demonstrated that this method is effective, the variances were reduced by more than one order of magnitude with the pointing accuracy significantly improved. It has been demonstrated that GP regression can be effectively and conveniently used as a powerful tool in pointing error compensations.
Acknowledgments
This work is supported by the National Key R&D Program of China (No.2017YFF0106401). The financial supports from the Natural Science Foundation of China (NSFC) under the grant 61701321 and that from the Natural Science Foundation of Shenzhen University (No. 860-000002110215) are also acknowledged.
References
- J.M. Hilkert, Inertially stabilized platform technology, IEEE Contr. Syst. Mag. 28, 26–46 (2008) [Google Scholar]
- M.K. Michael, Inertially stabilized platforms for optical imaging systems, IEEE Contr. Syst. Mag. 28, 47–64 (2008) [CrossRef] [Google Scholar]
- A.K. Rue, Calibration of precision gimballed pointing systems, IEEE Trans. Aero. Elec. Syst. AES 6, 697–706 (1970) [CrossRef] [Google Scholar]
- Q.J. Tang, X.J. Wang, Q. Yang, Static pointing error analysis of electro-optical detection systems, Proc. IMechE (2014) DOI: 10.1177/0954405414551107 [Google Scholar]
- R. Meeks, Improving telescope mechanical error estimates using pointing data, PhD Thesis, Colorado State University, USA, 2003 [Google Scholar]
- X. Zhou, H. Liu, Q. Liu, J. Lin, Modeling and optimization of the integrated TDICCD aerial camera pointing error, Appl. Opt. 59, 8196–8204 (2020) [CrossRef] [PubMed] [Google Scholar]
- X. Liang, J. Zhou, W. Ma, Method of distortion and pointing correction of a ground-based telescope, Appl. Opt. 58, 5136–5142 (2019) [CrossRef] [PubMed] [Google Scholar]
- F. Wu, S. Li, H. Zhu, C. An, J. Cai, P. Du, C. Wang, X. Cui, X. Yan, Analysis on the optical axis error of the spherical shell in the electro-optical system, Optik 168, 458–461 (2018) [CrossRef] [Google Scholar]
- Z.Y. Zhang, X.Y. Zhou, D.P. Fan, Analysis, modelling and correction of pointing errors for electro-optical detection systems, Acta Aeron. Astron. Sin. 32, 2042–2054 (2011) [Google Scholar]
- L. Huang, W.L. Ma, J.L. Huang, Modeling and calibration of pointing errors with alt-az telescope, New Astron. 47, 105–110 (2016) [CrossRef] [Google Scholar]
- C. Xu, W. Han, D. Wang, D. Huang, P. Yuan, Modeling and correction for the optical axis pointing error of an airborne electro-optical platform, Appl. Opt. 58, 6455–6463 (2019) [CrossRef] [PubMed] [Google Scholar]
- L.J. Yan, Y.M. Huang, Y.H. Zhang, Using Allan variance based semi-parameter model to calibrate pointing errors of alt-az telescopes, Appl. Sci. 8, 614 (2018) [CrossRef] [Google Scholar]
- H.J. Hong, X.Y. Zhou, Z.Y. Zhang, D.P. Fan, Modelling and calibration of pointing errors using a semi-parametric regression method with applications in inertially stabilized platforms, Proc. IMechE (2013) DOI:10.1177/0954405413475559 [Google Scholar]
- C. Williams, C. Rasmussen, Gaussian processes for regression, In Advances in Neural Information Processing Systems 8, 514–520 (1996) [Google Scholar]
- A. O'Hagan, Curve fitting and optimal design for prediction (with discussion), J. R. Stat. Soc. B 40, 1–42 (1978) [Google Scholar]
- C. Rasmussen, Gaussian processes in machine learning, Advanced Lectures on Machine Learning, Lecture Notes in Artificial Intelligence 3176, 63–71 (2004) [CrossRef] [Google Scholar]
- C. Rasmussen, C. Williams, Gaussian processes for machine learning (MIT Press, London, 2006) [Google Scholar]
- M. Ebden, Gaussian processes for regression: a quick introduction (University of Oxford, UK, 2008) [Google Scholar]
- C. Rasmussen, H. Nickisch, Gaussian processes for machine learning (GPML) Toolbox, J. Mach. Learn. Res. 11, 3011–3015 (2010) [Google Scholar]
Cite this article as: Qijian Tang, Qingping Yang, Xiangjun Wang, Alistair B. Forbes, Pointing error compensation of electro-optical detection systems using Gaussian process regression, Int. J. Metrol. Qual. Eng. 12, 22 (2021)
All Tables
All Figures
 |
Fig. 1 Test apparatus of the EODS. |
| In the text | |
 |
Fig. 2 Pointing error regression for azimuth and elevation. |
| In the text | |
 |
Fig. 3 Prediction results for the training data. |
| In the text | |
 |
Fig. 4 Prediction results for the test data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.